题目内容
9.有两种包装盒,大盒比小盒可多装20克某一物品.已知120克这一物品单独装满小盒比单独装满大盒多1盒.(1)问小盒每个可装这一物品多少克?
(2)现有装满这一物品两种盒子共50个.设小盒有n个,所有盒子所装物品的总量为w克.
①求w关于n的函数解析式,并写出定义域;
②如果小盒所装物品总量与大盒所装物品总量相同,求所有盒子所装物品的总量.
分析 (1)设小盒每个可装这一物品x克,根据题意,列出分式方程,求出x的值即可;
(2)①根据两种盒子的数量共有50个,所装物品的重量等于大盒物品质量之和+小盒物品质量之和;
②根据小盒所装物品总量与大盒所装物品总量相同列出n的方程,求出n的值即可.
解答 解:(1)设小盒每个可装这一物品x克,
根据题意得
$\frac{120}{x}$-$\frac{120}{x+20}$=1,
即x2+20x-2400=0,
解得x1=40,x2=-60,
它们都是原方程的解,但x=-60不合题意.
答:小盒每个可装这一物品40克.
(2)①w=40n+60(50-n)=3000-20n,(0<n<50,n为整数),
②40n=60(50-n),
解得n=30,
w=2400;
答:所有盒子所装物品的总量为2400克.
点评 本题主要考查了一次函数的应用以及分式方程的应用,解题的关键是根据题意列出分式方程求出每个小盒装物品的重量,此题难度不大.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
19.若把分式$\frac{2xy}{3x-y}$的x、y同时扩大为原来的3倍,则分式的值( )
| A. | 扩大3倍 | B. | 缩小3倍 | C. | 不变 | D. | 缩小6倍 |
1.下列命题中真命题有( )
①菱形的对角线互相垂直平分;②梯形的对角线相等;③矩形的对角线平分一组内角;④平行四边形对角线相等;⑤对角线相等的四边形是矩形;⑥对角线互相垂直的四边形都是菱形;⑦对角线互相平分的四边形是平行四边形;⑧对角线互相垂直平分四边形是正方形( )
①菱形的对角线互相垂直平分;②梯形的对角线相等;③矩形的对角线平分一组内角;④平行四边形对角线相等;⑤对角线相等的四边形是矩形;⑥对角线互相垂直的四边形都是菱形;⑦对角线互相平分的四边形是平行四边形;⑧对角线互相垂直平分四边形是正方形( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
18.已知x2-x-3=0,则x3-4x2+2017的值为( )
| A. | 2008 | B. | 2009 | C. | 2016 | D. | 2017 |
 如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.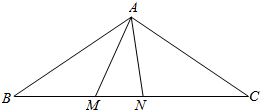 如图,△ABC中,AB=AC,∠B=36°,M,N是BC上两点,且∠AMN=∠ANM=2∠BAM,则图中的等腰三角形一共有( )
如图,△ABC中,AB=AC,∠B=36°,M,N是BC上两点,且∠AMN=∠ANM=2∠BAM,则图中的等腰三角形一共有( )