题目内容
19.若关于x的分式方程$\frac{2x-a}{x-2}$=$\frac{1}{2}$的解为非负数,则a的取值范围是a>1,且a≠4.分析 在方程的两边同时乘以2(x-2),解方程,用含a的式子表示出x的值,再根据x≥0,且x≠2,解不等于组即可.
解答 解:两边同时乘以2(x-2),
得:4x-2a=x-2,
解得x=$\frac{2a-2}{3}$,
由题意可知,x≥0,且x≠2,
∴$\left\{\begin{array}{l}{\frac{2a-2}{3}≥0}\\{\frac{2a-2}{3}≠2}\end{array}\right.$,解得:a≥1,且a≠4,
故答案为:a≥1,且a≠4.
点评 本题主要考查分式方程的解,解决此类问题时,通常先用含a的式子表示出x的值,再根据x的取值范围即可求出a的取值范围,但要注意分式的最简公分母不等于0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10. 如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
 如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )
如图,CE是△ABC的外角∠ACD的平分线,若∠B=35°,∠ACE=60°,则∠A=( )| A. | 95° | B. | 85° | C. | 75° | D. | 35° |
4.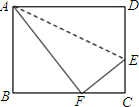 如图,沿AE折叠长方形ABCD,使点D恰落在BC边上的点F处,已知AB=8cm,BC=10cm,则CE的长为( )
如图,沿AE折叠长方形ABCD,使点D恰落在BC边上的点F处,已知AB=8cm,BC=10cm,则CE的长为( )
 如图,沿AE折叠长方形ABCD,使点D恰落在BC边上的点F处,已知AB=8cm,BC=10cm,则CE的长为( )
如图,沿AE折叠长方形ABCD,使点D恰落在BC边上的点F处,已知AB=8cm,BC=10cm,则CE的长为( )| A. | 5cm | B. | 4cm | C. | 3.5cm | D. | 3cm |
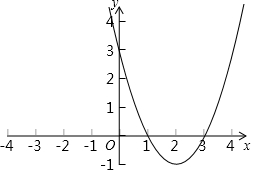 在平面直角坐标系xOy中,二次函数图象所在的位置如图所示:
在平面直角坐标系xOy中,二次函数图象所在的位置如图所示: 作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,其中,点A,B,C的坐标分别为A(-2,1),B(-4,5),C(-5,2).
作图题:(不要求写作法)如图,△ABC在平面直角坐标系中,其中,点A,B,C的坐标分别为A(-2,1),B(-4,5),C(-5,2). 如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,则MN的值是5cm.
如图,已知点C在线段AB上,且AC=6cm,BC=4cm,点M,N分别是AC,BC的中点,则MN的值是5cm.