题目内容
10．
如图，CE是△ABC的外角∠ACD的平分线，若∠B=35°，∠ACE=60°，则∠A=（ ）| A． | 95° | B． | 85° | C． | 75° | D． | 35° |
分析 根据角平分线的定义求出∠ACD，根据三角形的外角的性质计算即可．
解答 解：∵CE是△ABC的外角∠ACD的平分线，
∴∠ACD=2∠ACE=120°，
∴∠A=∠ACD-∠B=85°，
故选：B．
点评 本题考查的是三角形的外角的性质、角平分线的定义，掌握三角形的一个外角等于和它不相邻的两个内角的和是解题的关键．
练习册系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
如图，已知∠ACD是△ABC的一个外角，∠ACD=130°，∠B=70°，则∠A的度数为60°．
18．下列图形是四种运动品牌的商标，其中是轴对称图形的是（ ）
| A． |  | B． |  | C． |  | D． |  |
5．
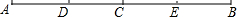如图，C是AB的中点，D、E分别是AC、BC的中点，下列结论错误的是（ ）
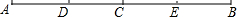如图，C是AB的中点，D、E分别是AC、BC的中点，下列结论错误的是（ ）| A． | AC=2CE | B． | AB-AD=2CD | C． | AD=$\frac{1}{3}$DB | D． | DE=$\frac{1}{2}$AB |
15．△ABC与△DEF的相似比为1：3，则△ABC和△DEF的面积比为（ ）
| A． | 1：$\sqrt{3}$ | B． | $\sqrt{3}$：1 | C． | 9：1 | D． | 1：9 |
20．单项式-$\frac{5x{y}^{2}}{3}$的系数与次数分别是（ ）
| A． | -5，2 | B． | -$\frac{1}{3}$，3 | C． | -$\frac{5}{3}$，2 | D． | -$\frac{5}{3}$，3 |