题目内容
4．
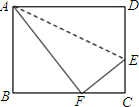如图，沿AE折叠长方形ABCD，使点D恰落在BC边上的点F处，已知AB=8cm，BC=10cm，则CE的长为（ ）| A． | 5cm | B． | 4cm | C． | 3.5cm | D． | 3cm |
分析 如图，根据勾股定理求出BF的长；进而求出FC的长度；由题意得EF=DE；利用勾股定理列出关于EC的方程，解方程即可解决问题．
解答 解：∵四边形ABCD为矩形，
∴DC=AB=8；∠B=∠C=90°；
由题意得：AF=AD=10，EF=DE=m，EC=8-m；
由勾股定理得：BF2=102-82，
∴BF=6，CF=10-6=4；
在△EFC中，由勾股定理得：m2=42+（8-m）2，
解得：m=5，EC=8-5=3．
故选D．
点评 该题主要考查了翻折变换、矩形的性质、勾股定理等知识，解题的关键是灵活运用有关定理来分析、判断、推理或解答．
练习册系列答案
相关题目
14．若（x-3）（x2+ax+b）的积中不含x的二次项和一次项，则a和b的值（ ）
| A． | a=0；b=2 | B． | a=3；b=9 | C． | a=-1；b=2 | D． | a=2；b=4 |
15．△ABC与△DEF的相似比为1：3，则△ABC和△DEF的面积比为（ ）
| A． | 1：$\sqrt{3}$ | B． | $\sqrt{3}$：1 | C． | 9：1 | D． | 1：9 |
12．下列代数式中，既不是单项式，也不是多项式的是（ ）
| A． | 2x2-1 | B． | -$\frac{7}{3}$xy | C． | $\frac{b}{a}$ | D． | 0 |
将正整数按如图所示的规律排列下去，若用有序数对（m，n）表示从上到下第m排，从左到右第n个数，如（4，2）表示整数8，则（11，5）表示的数是60．