题目内容
11.(1)化简(a-b)(4a-b)+3a(4a-b).(2)若(1)中的b=ka,则(1)的结果,能否等于a2,若能请求出所有的k值,若不能,说明理由.
分析 (1)先算乘法,再合并同类项即可;
(2)代入后合并同类项,得出方程,求出k即可.
解答 解:(1)原式=4a2-ab-4ab+b2+12a2-3ab
=16a2-8ab+b2;
(2)能,
当b=ka时,原式=16a2-8ka2+(ka)2
=(16-8k+k2)a2,
根据题意得:16-8k+k2=1,
k2-8k+15=0,
解得:k=3或5.
点评 本题考查了整式的混合运算和求值,能正确根据整式的运算法则进行化简是解此题的关键.

练习册系列答案
相关题目
6. 如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
 如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
如图,四边形ABCD中,AD=CD,AB=CB,则如下结论:①AC垂直平分BD,②BD垂直平分AC,③△ABD≌△CBD,④AO=OC=$\frac{1}{2}$AC,其中正确结论的序号有②③④.
3.-5的相反数是( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | 5 | D. | -5 |
20.单项式-$\frac{5x{y}^{2}}{3}$的系数与次数分别是( )
| A. | -5,2 | B. | -$\frac{1}{3}$,3 | C. | -$\frac{5}{3}$,2 | D. | -$\frac{5}{3}$,3 |
 如图,已知∠ACD是△ABC的一个外角,∠ACD=130°,∠B=70°,则∠A的度数为60°.
如图,已知∠ACD是△ABC的一个外角,∠ACD=130°,∠B=70°,则∠A的度数为60°. 将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8,则(11,5)表示的数是60.
将正整数按如图所示的规律排列下去,若用有序数对(m,n)表示从上到下第m排,从左到右第n个数,如(4,2)表示整数8,则(11,5)表示的数是60.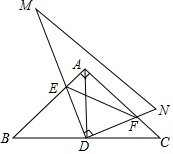 将一副三角板按如图摆放,其中△ABC为含有45度角的三角板,直线AD是等腰直角三角形ABC的对称轴,且将△ABC分成两个等腰直角三角形,DM、DN分别与边AB、AC交于E、F两点,有下列四个结论:①BD=AD=CD②△AED≌△CFD③BE+CF=EF④S四边形AEDF=$\frac{1}{4}$AB2.其中正确结论是①②④(填写正确序号)
将一副三角板按如图摆放,其中△ABC为含有45度角的三角板,直线AD是等腰直角三角形ABC的对称轴,且将△ABC分成两个等腰直角三角形,DM、DN分别与边AB、AC交于E、F两点,有下列四个结论:①BD=AD=CD②△AED≌△CFD③BE+CF=EF④S四边形AEDF=$\frac{1}{4}$AB2.其中正确结论是①②④(填写正确序号)