题目内容
15.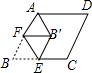 如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )
如图所示,在菱形ABCD中,BC=2,∠B=60°,E为BC的中点,点F在AB边上,连接EF,将△BEF沿EF翻折,使点B落在点B′处,连接AB′,则AB′的最小值是( )| A. | 2-$\sqrt{3}$ | B. | $\sqrt{3}$+1 | C. | 2+$\sqrt{3}$ | D. | $\sqrt{3}$-1 |
分析 如图所示,连接AC,AE,当A、B′、E共线时,AB′最小,只要求出AE即可解决问题.
解答 解:如图所示,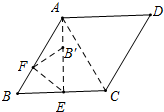 连接AC,AE,
连接AC,AE,
∵四边形ABCD是菱形,
∴AB=BC,∵∠B=60°,
∴△ABC是等边三角形,
∵BE=EC,
∴AE⊥BC,
∵BC=2,∠BAE=30°,
∴AE=$\sqrt{3}$,BE=1,
∵当A、B′、E共线时,AB′最小(垂线段最短),
∴AB′最小值=AE-BE′=AE-BE=$\sqrt{3}$-1.
故选D.
点评 此题主要考查了菱形的性质以及直角三角形30度角性质,垂线段最短等知识,得出B′点位置是解题关键,属于中考常考题型.

练习册系列答案
相关题目
6.下列命题中,真命题是( )
| A. | 有两边相等的平行四边形是菱形 | |
| B. | 有一个角是直角的四边形是矩形 | |
| C. | 四个角相等的菱形是正方形 | |
| D. | 两条对角线互相垂直且相等的四边形是正方形 |
3.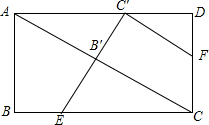 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
 如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )
如图,在矩形ABCD中,点E在BC上,将△ABE沿AE翻折,点B恰好落在对角线AC上的B′处,点F在CD上,将△ECF沿EF翻折,点C恰好落在AD上的C′处,若E、B′C′三点共线,则$\frac{CF}{AB}$=( )| A. | $\frac{\sqrt{2}}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{3}{4}$ |
10.若不等式组$\left\{\begin{array}{l}{x<2a-1}\\{x>3}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤2 | B. | a>2 | C. | a>3 | D. | a≥3 |
4.下列说法正确的是( )
| A. | 掷一枚质地均匀的正方体骰子,骰子停止转动后,5点朝上是必然事件 | |
| B. | 审查书稿中有哪些学科性错误适合用抽样调查法 | |
| C. | 甲乙两人在相同条件下各射击10次,他们的成绩的平均数相同,方差分别是S甲2=0.4,S乙2=0.6,则甲的射击成绩较稳定 | |
| D. | 掷两枚质地均匀的硬币,“两枚硬币都是正面朝上”这一事件发生的概率为$\frac{1}{2}$ |
5.成都地铁自开通以来,发展速度不断加快,现已成为成都市民主要出行方式之一.今年4月29日成都地铁安全运输乘客约181万乘次,又一次刷新客流纪录,这也是今年以来第四次客流纪录的刷新,用科学记数法表示181万为( )
| A. | 18.1×105 | B. | 1.81×106 | C. | 1.81×107 | D. | 181×104 |
 在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.
在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128. 如图所示的两段弧中,位于上方的弧半径为r上,下方的弧半径为r下,则r上<r下.(填“<”“=”“>”)
如图所示的两段弧中,位于上方的弧半径为r上,下方的弧半径为r下,则r上<r下.(填“<”“=”“>”)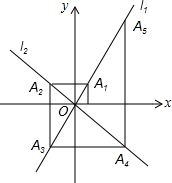 如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).
如图,在平面直角坐标系中,函数y=2x和y=-x的图象分别为直线l1,l2,过点(1,0)作x轴的垂线交l1于点A1,过点A1作y轴的垂线交l2于点A2,过点A2作x轴的垂线交l1于点A3,过点A3作y轴的垂线交l2于点A4,…依次进行下去,则点A2017的坐标为(21008,21009).