题目内容
20.已知a+$\frac{1}{a}$=$\sqrt{7}$,则a-$\frac{1}{a}$的值为( )| A. | 7 | B. | 4 | C. | ±$\sqrt{3}$ | D. | ±3 |
分析 将a+$\frac{1}{a}$=$\sqrt{7}$求得a2+$\frac{1}{{a}^{2}}$=5,将其代入到(a-$\frac{1}{a}$)2=a2+$\frac{1}{{a}^{2}}$-2中,再开方可得答案.
解答 解:∵a+$\frac{1}{a}$=$\sqrt{7}$,
∴(a+$\frac{1}{a}$)2=7,即a2+2+$\frac{1}{{a}^{2}}$=7,
∴a2+$\frac{1}{{a}^{2}}$=5,
则(a-$\frac{1}{a}$)2=a2+$\frac{1}{{a}^{2}}$-2=3,
∴a-$\frac{1}{a}$=±$\sqrt{3}$,
故选:C.
点评 本题主要考查分式的化简求值和完全平方公式,由原式得出a2+$\frac{1}{{a}^{2}}$的值是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
10.若不等式组$\left\{\begin{array}{l}{x<2a-1}\\{x>3}\end{array}\right.$无解,则a的取值范围是( )
| A. | a≤2 | B. | a>2 | C. | a>3 | D. | a≥3 |
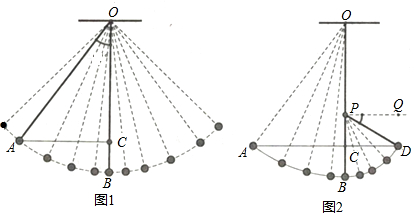

 在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128.
在直角坐标系中,直线y=x+1与y轴交于点A1,按如图方式作正方形A1B1C1O、A2B2C2C1、A3B3C1C2…,A1、A2、A3…在直线y=x+1上,点C1、C2、C3…在x轴上,图中阴影部分三角形的面积从左到右依次记为S1、S2、S3、…,则S5的值为128. 某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路:
某校数学兴趣小组在探究如何求tan 15°,cos15°的值,经过自主思考、合作交流讨论,得到以下思路: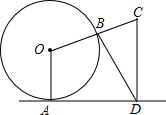 如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.
如图,直线l与⊙O相切于点A,作半径OB并延长至点C,使得BC=OB,作CD⊥直线l于点D,连接BD得∠CBD=75°,则∠OCD=70度.