题目内容
18.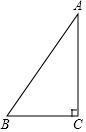 如图,在△ABC 中,∠C=90°
如图,在△ABC 中,∠C=90°(1)利用尺规作∠B 的角平分线交AC于D,以BD为直径作⊙O交AB于E(保留作图痕迹,不写作法);
(2)综合应用:在(1)的条件下,连接DE
①求证:CD=DE;
②若sinA=$\frac{3}{5}$,AC=6,求AD.
分析 (1)根据题意作出图形即可;
(2)有BD为⊙O的直径;得到∠BED=90°,根据角平分线的性质即可得到结论;
(3)解直角三角形即可得到结论.
解答 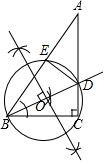 解:(1)如图所示,
解:(1)如图所示,
(2)∵BD为⊙O的直径;
∴∠BED=90°,
又∵∠C=90°;
∴DE⊥AB,DC⊥BC;
又∵BD平分∠ABC;
∴DE=DC;
(3)在Rt△ADE中,sinA=$\frac{DE}{AD}$
∵sinA=$\frac{3}{5}$
∴$\frac{DE}{AD}$=$\frac{3}{5}$
设DC=DE=3x,AD=5x
∵AC=AD+DC
∴3x+5x=6x=$\frac{3}{4}$
AD=5x=5×$\frac{3}{4}$=$\frac{15}{4}$
点评 本题考查了作图-复杂作图,圆周角定理,解直角三角形,正确的作出图形是解题的关键.

练习册系列答案
相关题目
10.已知命题A:“带根号的数都是无理数”.在下列选项中,可以作为判断“命题A是假命题”的反例的是( )
| A. | $\sqrt{3}$ | B. | $\root{3}{2}$ | C. | $\sqrt{4}$ | D. | $\sqrt{8}$ |
7.已知矩形ABCD中,AB=2$\sqrt{3}$-$\sqrt{2}$,BC=$\sqrt{6}$+1,则矩形ABCD的面积是( )
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{3}$-$\sqrt{2}$ | C. | 5$\sqrt{2}$-4$\sqrt{3}$ | D. | 5$\sqrt{2}$+4$\sqrt{3}$ |
8.下列命题正确的是( )
| A. | △ABC中,∠A、∠B、∠C的对边分别为a、b、c.若a2+b2=c2 则∠B=90° | |
| B. | 如果一个三角形两边的平方差等于第三边的平方,那么这个三角形是直角三角形 | |
| C. | 直角三角形中,两条边的平方和等于第三边的平方 | |
| D. | △ABC中,若a=3、b=4则c=5 |
 在如图所示的4×4方格中,每个小方格的边长都为1
在如图所示的4×4方格中,每个小方格的边长都为1 如图,在矩形ABCD中,连接对角线AC,BD,延长BC至点E,使BC=CE,连接DE.求证:DE=AC.
如图,在矩形ABCD中,连接对角线AC,BD,延长BC至点E,使BC=CE,连接DE.求证:DE=AC.