题目内容
17.顺次连接菱形的四边中点所得的图形为矩形.分析 根据中位线性质可知:EH是△ADC的中位线,FG是△BAC的中位线,则EH∥AC,FG∥AC,得EH∥FG,同理另两边也平行,证得四边形EFGH是平行四边形,再证明∠FEH=90°,则中点四边形是矩形.
解答 解:菱形ABCD中,E、F、G、H分别是AD、AB、BC、CD的中点,则AC⊥BD,
∴EH∥AC,FG∥AC,
∴EH∥FG,
同理得EF∥HG,
∴四边形EFGH是平行四边形,
同理得:四边形ENOM是平行四边形,
∴∠FEH=∠NOM=90°,
∴?EFGH是矩形,
∴顺次连结菱形四边中点所得的四边形一定是矩形;
故答案是:矩形.
点评 本题考查了中点四边形和菱形的性质,运用三角形中位线的性质:三角形的中位线平行于第三边,且等于第三边的一半;先证明中点四边形为平行四边形,再利用菱形对角线互相垂直的特性得出结论.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案
相关题目
5.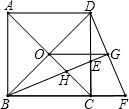 如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
 如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )
如图,O为正方形ABCD对角线BD的中点,BE平分∠DBC,交DC于点E,延长BC到点F,使CF=CE,连接DF,交BE的延长线于点G,连接OG、OC,OC交BG于点H.下面四个结论中不正确的是( )| A. | △BCE≌△DCF | B. | OG∥AD | C. | BH=GH | D. | OG=$\frac{1}{2}$BD |
7.已知矩形ABCD中,AB=2$\sqrt{3}$-$\sqrt{2}$,BC=$\sqrt{6}$+1,则矩形ABCD的面积是( )
| A. | 5$\sqrt{2}$ | B. | 4$\sqrt{3}$-$\sqrt{2}$ | C. | 5$\sqrt{2}$-4$\sqrt{3}$ | D. | 5$\sqrt{2}$+4$\sqrt{3}$ |
 请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$.
请在方格内画△ABC,使它的顶点都在格点上,且三边长分别为$\sqrt{2}$,$\sqrt{10}$,4$\sqrt{\frac{1}{2}}$. 在如图所示的4×4方格中,每个小方格的边长都为1
在如图所示的4×4方格中,每个小方格的边长都为1