题目内容
16.若∠ACB=a,∠EAC=b,∠FBC=c.(1)如图1,若AE∥BF,则a,b,c之间有何关系?a=b+c(直接写出结果)
(2)如图2,AM是∠EAC的平分线,BN是∠FBC的平分线,若AM∥BN,则a,b,c之间有何关系?并说明理由.
(3)如图3,若∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,试探究∠APB与a,b,c之间的关系是∠APB=a-$\frac{1}{2}$(b+c)(用a,b,c表示)
(4)如图4,若a≥b+c,∠EAC与∠FBC的平分线相交于P1,∠EAP1与∠FBP1的平分线交于P2;依此类推,则∠P6=a-$\frac{63}{64}$(b+c).(用a、b、c表示),写出结论即可.

分析 (1)过点C作CM∥AE,根据平行线的性质即可得出∠EAC=∠ACM、∠FBC=∠BCM,再通过角的计算即可得出结论;
(2)a=$\frac{1}{2}$(b+c).过点C作CG∥AM,根据平行线的性质可得出∠MAC=∠ACG、∠NBC=∠BCG,再根据角平分线的性质结合角的计算即可得出结论;
(3)连接PC并延长到点M,根据三角形外角的性质可得出∠ACM=∠PAC+∠APC、∠BCM=∠PBC+∠BPC,再根据角平分线的性质结合角的计算即可得出结论;
(4)结合(3)的结论找出∠P1、∠P2、∠P3,根据角的变化找出变化规律“∠Pn=a-$\frac{{2}^{n}-1}{{2}^{n}}$(b+c)”,依此规律即可得出结论.
解答 解:(1)过点C作CM∥AE,如图1所示.
∵CM∥AE,
∴∠EAC=∠ACM.
∵CM∥AE,AE∥BF,
∴CM∥BF,
∴∠FBC=∠BCM.
∵∠ACB=∠ACM+∠BCM=a,∠EAC=b,∠FBC=c,
∴a=b+c.
故答案为:a=b+c.
(2) a=$\frac{1}{2}$(b+c).理由如下:
a=$\frac{1}{2}$(b+c).理由如下:
过点C作CG∥AM,如图2所示.
∵CG∥AM,AM∥BN,
∴AM∥BN∥CG,
∴∠MAC=∠ACG,∠NBC=∠BCG,
∵AM是∠EAC的平分线,BN是∠FBC的平分线,
∴∠ACB=∠ACG+∠BCG=∠MAC+∠NBC=$\frac{1}{2}$∠EAC+$\frac{1}{2}$∠FBC=$\frac{1}{2}$(∠EAC+∠FBC)=$\frac{1}{2}$(b+c).
(3)连接PC并延长到点M,如图3所示.
∵∠EAC的平分线所在直线与∠FBC平分线所在直线交于P,
∴∠PAC=$\frac{1}{2}$∠EAC,∠PBC=$\frac{1}{2}$∠FBC,
∵∠ACM=∠PAC+∠APC,∠BCM=∠PBC+∠BPC,∠ACB=∠ACM+∠BCM,∠APB=∠APC+∠BPC,
∴∠ACB=∠PAC+∠PBC+∠APB,
∵∠ACB=a,∠EAC=b,∠FBC=c,
∴a=$\frac{1}{2}$(b+c)+∠APB,
∴∠APB=a-$\frac{1}{2}$(b+c).
故答案为:∠APB=a-$\frac{1}{2}$(b+c).
(4)结合(3)结论可知:
∠P1=a-$\frac{1}{2}$(b+c),∠P2=a-$\frac{3}{4}$(b+c),∠P3=a-$\frac{7}{8}$(b+c),…,
∴∠Pn=a-$\frac{{2}^{n}-1}{{2}^{n}}$(b+c).
当n=6时,∠P6=a-$\frac{{2}^{6}-1}{{2}^{6}}$(b+c)=a-$\frac{63}{64}$(b+c).
故答案为:a-$\frac{63}{64}$(b+c).
点评 本题考查了平行线的性质.角平分线的性质、角的计算、三角形外角的性质以及规律型中数的变化规律,解题的关键是:(1)找出∠ACB=∠EAC+∠FBC;(2)找出∠ACB=$\frac{1}{2}$∠EAC+$\frac{1}{2}$∠FBC;(3)根据三角形外角的性质找出∠ACB=∠PAC+∠PBC+∠APB;(4)找出规律“∠Pn=a-$\frac{{2}^{n}-1}{{2}^{n}}$(b+c)”.本题属于中档题,难度不大,解决该题型题目时,根据平行线的性质找出相等或互补的角是关键.

 名校课堂系列答案
名校课堂系列答案| A. | y=(x-4)2-6 | B. | y=(x-4)2-2 | C. | y=(x-2)2-2 | D. | y=(x-1)2-3 |
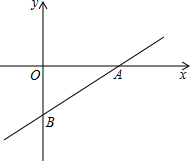 如图,直线y=$\frac{3}{4}$x-3交x轴于点A,交y轴于点B.已知x轴上某一点C到直线y=$\frac{3}{4}$x-3的距离为5,则点C的坐标为($\frac{37}{3}$,0)或(-$\frac{13}{3}$,0).
如图,直线y=$\frac{3}{4}$x-3交x轴于点A,交y轴于点B.已知x轴上某一点C到直线y=$\frac{3}{4}$x-3的距离为5,则点C的坐标为($\frac{37}{3}$,0)或(-$\frac{13}{3}$,0).
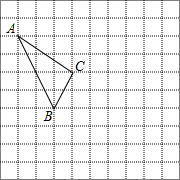 在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,4),(-1,2).
在如图所示的正方形网格中,每个小正方形的边长为1,格点三角形(顶点是网格线的交点的三角形)ABC的顶点A、C的坐标分别为(-4,4),(-1,2).