Question

4．解不等式组：$\left\{\begin{array}{l}{\frac{2x+1}{3}＞x-1}\\{3（x-2）≥x-4}\end{array}\right.$，并写出它的所有整数解．

Answer 1

分析 首先解每个不等式，把解集在数轴上表示出来即可得到不等式组的解集，然后确定解集中的整数即可．

解答 解：$\left\{\begin{array}{l}{\frac{2x+1}{3}＞x-1…①}\\{3（x-2）≥x-4…②}\end{array}\right.$，
解①得x＜4，
解②得x≥1．

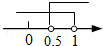
不等式组的解集是1≤x＜4．
则整数解是1，2，3．

点评 本题考查了一元一次不等式组的解法：解一元一次不等式组时，一般先求出其中各不等式的解集，再求出这些解集的公共部分，利用数轴可以直观地表示不等式组的解集．方法与步骤：①求不等式组中每个不等式的解集；②利用数轴求公共部分．解集的规律：同大取大；同小取小；大小小大中间找；大大小小找不到．