题目内容
16. 如图,AD是△ABC中线,E是AD上一点,∠BED=∠CAD,求证:BE=AC.
如图,AD是△ABC中线,E是AD上一点,∠BED=∠CAD,求证:BE=AC.
分析 延长AD到G,使DG=AD,连接BG,由已知AD是BC边上的中线,所以推出△BDG≌△CDA,则得到,∠G=∠CAD,BG=AC,再想法证BG=BE,已知∠BED=∠CAD,所以∠G=∠BED,即BG=BE,故AC=BE.
解答 证明:如图,
延长AD到G,使DG=AD,连接BG,
∵在△BDG和△CDA中,
$\left\{\begin{array}{l}{DG=AD}\\{∠BDG=∠ADC}\\{BD=CD}\end{array}\right.$
∴△BDG≌△CDA,
∴∠G=∠CAD,BG=AC,
∵∠BED=∠CAD,
∴∠G=∠BED,
∴BG=BE,
∴AC=BE.
点评 此题考查全等三角形的判定和性质,解答此题的关键是先作辅助线构三角形全等,通过等量代换得证.

练习册系列答案
相关题目
6.计算(-x2y3)3•(-xy2)的结果是( )
| A. | -x7y11 | B. | x7y11 | C. | x6y8 | D. | -x7y8 |
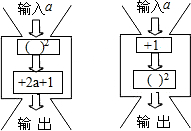 分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?
分别给下面的两台数值转化机输入5个数据,比较它们的输出结果,你发观了什么规律?