题目内容
11.已知:3m=a,3n=b,用a、b表示3m+n和32m+3n.分析 根据同底数幂的乘法底数不变指数相加,可得答案;
根据幂的乘方,可得同底数幂的乘法,根据同底数幂的乘法,可得答案.
解答 解:3m+n=3m×3n=ab;
32m=(3m)2=a2,33n=(3n)3=b3,
32m+3n=32m×33n=a2•b3=a2b3.
点评 本题考查了同底数幂的乘法,利用幂的乘方得出同底数幂的乘法是解题关键.

练习册系列答案
相关题目
19.如下表是通讯公司推出的移动电话两种计费方式:
设一个月内使用移动电话主叫的时间为t(t为正整数)分钟,请根据表中提供的信息回答下列问题:
(1)用含有t的式子填写下表:
(2)当t为何值时,两种计费方式的费用相等?
(3)根据以上的计算,写出t为何值时选择方案一更省钱.
| 月使用费 单位:元 | 主叫限制时间 单位:分 | 主叫超时费 单位:分 | 被叫 | |
| 方式一 | 30 | 150 | 0.25 | 免费 |
| 方式二 | 50 | 350 | 0.16 | 免费 |
(1)用含有t的式子填写下表:
| t≤150 | 150<t<350 | t=350 | t>350 | |
| 方式一 计费/元 | 30 | 0.25t-7.5 | 80 | 0.25t-7.5 |
| 方式二 计费/元 | 50 | 50 | 50 | 0.16t-6 |
(3)根据以上的计算,写出t为何值时选择方案一更省钱.
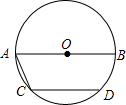 如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长.
如图,AB是⊙O直径,CD是弦,AB∥CD,且AB=30cm,CD=24cm,求弦AC的长. 如图,AD是△ABC中线,E是AD上一点,∠BED=∠CAD,求证:BE=AC.
如图,AD是△ABC中线,E是AD上一点,∠BED=∠CAD,求证:BE=AC. 如图,a,b,c是数轴上三个点A、B、C所对应的实数,|a|<|c|,试化简:($\sqrt{c}$)2+|a-b|+$\root{3}{(a+b)^{3}}$-|a+c|
如图,a,b,c是数轴上三个点A、B、C所对应的实数,|a|<|c|,试化简:($\sqrt{c}$)2+|a-b|+$\root{3}{(a+b)^{3}}$-|a+c|