题目内容
16. 已知AB为⊙O的直径,点C是⊙O上的一点CH⊥AB于点H,过点B作O的切线,交弦AC的延长线于点D,点E为CH的中点,连按AE并延长交BD于点F,直线CF交AB的延长线于点G.
已知AB为⊙O的直径,点C是⊙O上的一点CH⊥AB于点H,过点B作O的切线,交弦AC的延长线于点D,点E为CH的中点,连按AE并延长交BD于点F,直线CF交AB的延长线于点G.(1)求证:CG是⊙O的切线;
(2)若FB=FE=6,求⊙O的半径.
分析 (1)连接OC、OF、BC,证△OCF≌△OBF即可;
(2)根据FE=FB=FC可推出△FAG是等腰三角形,进而BG就等于直径;根F是DB中点可得OF∥AC,由平行线分线段成比例可算出FG,再由勾股定理算出BG即可.
解答 解:(1)如图,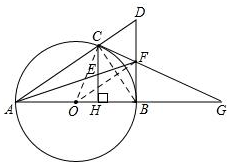
∵AB是⊙O的直径,BD是⊙O的切线,
∴AB⊥BD,
∵CH⊥AB,
∴CH∥BD,
∴$\frac{CE}{DF}=\frac{AE}{AF}=\frac{EH}{BF}$,
∵CE=EH,
∴DF=BF,
连接BC,则BC⊥AD,
∴CF=BF=DF,
连接OC、OF,
在△OCF和△OBF中,
$\left\{\begin{array}{l}{OC=OB}\\{OF=OF}\\{FC=FB}\end{array}\right.$
∴△OCF≌△OBF(SSS),
∴∠OCF=∠OBF=90°,
∴CG是⊙O的切线;
(2)∵FE=FB=6,
∴FC=FE=6,
∴∠FEC=∠FCE,
∵∠FCE+∠G=∠FEC+∠FAB=90°,
∴∠FAB=∠G,
∴FA=FG,
∴AB=BG,
∵AO=OB,
∴OF∥AC,
∴$\frac{GF}{FC}=\frac{GO}{OA}=3$,
∴FG=3FC=18,
∴BG=12$\sqrt{2}$,
∴OA=OB=$\frac{1}{2}AB=\frac{1}{2}BG=6\sqrt{2}$.
点评 本题考查了圆的切线的判定、圆周角的性质、平行线分线段成比例、直角三角形斜边中线、等腰三角形的判定与性质、勾股定理等众多知识点,有一定难度.熟悉圆的基本性质是解答的关键.

练习册系列答案
相关题目

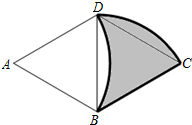 如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.
如图,已知△ABD与△BCD都是边长为3厘米的等边三角形,以A为圆心,AB长为半径画弧BD;以B为圆心,BC长为半径画弧CD,求阴影部分图形的周长.