题目内容
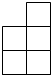
7.如图∠MON=120°,OP平分∠MON.点C是OP上一点,A、B分别是OM、ON上的点,∠ACB=60°.(1)图①中,AC⊥OM,BC⊥ON,则OA+OB的值等于哪线段的长?为什么?
(2)图②中,仍保持∠ACB的度数不变,A、B的位置变了,(1)中的结论还成立吗?请说明理由.
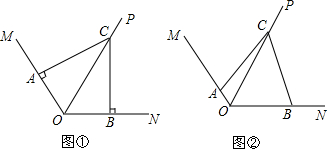
分析 (1)OA+OB=OC,根据角平分线的定义得到∠AOC=∠BOC=60°,由垂直的定义得到∠OAC=∠OBC=90°,根据三角形的内角和得到∠ACO=∠BCO=30°,根据直角三角形的性质得到OA=$\frac{1}{2}$OC,OB=$\frac{1}{2}$OC,即可得到结论;
(2)(1)中的结论成立,过C作CF⊥OM于F,CE⊥ON于E,得到∠CFO=∠CEO=90°,根据角平分线的性质得到∠AOC=∠BOC=60°,CF=CE,求得∠FCO=∠ECO=30°,于是得到OF=$\frac{1}{2}$OC,OE=$\frac{1}{2}$OC,∠FCE=60°,推出△ACF≌△BCE,根据全等三角形的性质得到AF=BE,等量代换得到OA+OB=OE+OF=OC.
解答 解:(1)OA+OB=OC,
∵∠MON=120°,OP平分∠MON,
∴∠AOC=∠BOC=60°,
∵AC⊥OM,BC⊥ON,
∴∠OAC=∠OBC=90°,
∴∠ACO=∠BCO=30°,
∴OA=$\frac{1}{2}$OC,OB=$\frac{1}{2}$OC,
∴OA+OB=0C;
(2)(1)中的结论成立, 过C作CF⊥OM于F,CE⊥ON于E,
过C作CF⊥OM于F,CE⊥ON于E,
∴∠CFO=∠CEO=90°,
∵∠MON=120°,OP平分∠MON,
∴∠AOC=∠BOC=60°,CF=CE,
∴∠FCO=∠ECO=30°,
∴OF=$\frac{1}{2}$OC,OE=$\frac{1}{2}$OC,∠FCE=60°,
∴OE=OF,
∵∠ACB=60°,
∴∠ACF=∠BCE,
在△ACF与△BCE中,$\left\{\begin{array}{l}{∠ACF=∠BCE}\\{CF=CE}\\{∠AFC=∠BEC}\end{array}\right.$,
∴△ACF≌△BCE,
∴AF=BE,
∴OA+OB=OE+OF=OC.
点评 本题考查了全等三角形的判定和性质,角平分线的性质,直角三角形的性质,正确的作出辅助线构造全等三角形是解题的关键.


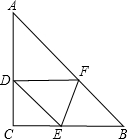 如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.
如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.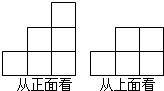 由若干个(大于8个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )
由若干个(大于8个)大小相同的正方体组成一个几何体的从正面看和从上面看如图所示,则这个几何体的从左面看不可能是下列图中的( )