题目内容
12.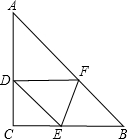 如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.
如图,在等腰直角三角形ABC中,AC=BC=2,∠C=90°,将△ABC折叠,使顶点B落在线段AC上的点D处,折痕为EF,如果△DEF为等腰三角形,则BE的长为4-2$\sqrt{2}$或1或2.
分析 根据折叠的性质得到DF=BF,BE=DE,∠FDE=∠B=45°,①当DF=DE时,则四边形DEBF是菱形,由平行线的性质得到∠DEC=∠B=45°,推出△DEC是等腰直角三角形,根据等腰直角三角形的性质得到BE=DE=$\sqrt{2}$CE,于是得到BE=4-2$\sqrt{2}$,②当DE=EF时,即BE=EF,根据折叠的性质得到D与C重合,根据线段垂直平分线的性质得到BE=$\frac{1}{2}$BC=1,③当DF=EF时,即EF=BF,点D与点A重合,E与C重合.
解答 解:∵将△ABC折叠,使顶点B落在线段AC上的点D处,
∴DF=BF,BE=DE,∠FDE=∠B=45°,
①当DF=DE时,则四边形DEBF是菱形,
∴DE∥AB,
∴∠DEC=∠B=45°,
∴△DEC是等腰直角三角形,
∴BE=DE=$\sqrt{2}$CE,
∵BC=2,∴CE+$\sqrt{2}$CE=2,
∴CE=2$\sqrt{2}$-2,
∴BE=4-2$\sqrt{2}$,
②当DE=EF时,即BE=EF,
∵∠B=45°,∴∠FEB=90°,
∴D与C重合,
∴E是BC的中点,
∴BE=$\frac{1}{2}$BC=1,
③当DF=EF时,即EF=BF,
∵∠B=45°,
∴∠FEB=45°,
∴∠EFD=90°,
∴点D与点A重合,E与C重合,
∴BE=BC=2,
故BE的长为4-2$\sqrt{2}$或1或2,.
故答案为:4-2$\sqrt{2}$或1或2.
点评 本题考查了翻折变换-折叠问题,等腰直角三角形的性质,熟练掌握折叠的性质是解题的关键,注意分类讨论.

练习册系列答案
相关题目
3.下列各组中的两个代数式为同类项的是( )
| A. | 3m2n与-m2n3 | B. | $\frac{1}{2}xy$与22yx | C. | 53与a3 | D. | 23x与2x3 |
4. 直线AB与⊙O相切于点A,如图,若∠OBA=60°,AB=1,则⊙O的半径为( )
直线AB与⊙O相切于点A,如图,若∠OBA=60°,AB=1,则⊙O的半径为( )
 直线AB与⊙O相切于点A,如图,若∠OBA=60°,AB=1,则⊙O的半径为( )
直线AB与⊙O相切于点A,如图,若∠OBA=60°,AB=1,则⊙O的半径为( )| A. | $\sqrt{5}$ | B. | $\sqrt{3}$ | C. | 1 | D. | 2 |
 如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,下面四个结论:①DA平分∠EDF;②EB=FC;③AD上的点到B、C两点的距离相等;④到AE、AF距离相等的点,到DE、DF的距离也相等,其中正确的结论有①②③④.(填序号)
如图,在△ABC中,AB=AC,AD是∠BAC的平分线,DE⊥AB于点E,DF⊥AC于点F,下面四个结论:①DA平分∠EDF;②EB=FC;③AD上的点到B、C两点的距离相等;④到AE、AF距离相等的点,到DE、DF的距离也相等,其中正确的结论有①②③④.(填序号)