Question

16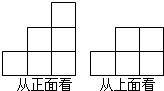．由若干个（大于8个）大小相同的正方体组成一个几何体的从正面看和从上面看如图所示，则这个几何体的从左面看不可能是下列图中的（　　）

• A．
• B．
• C．
• D．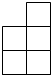

Answer 1

分析 由俯视图可得该组合几何体最底层正方体的个数及摆放形状，由主视图结合选项中所给的左视图看正方体的个数，即可解答本题．

解答 解：∵俯视图中有5个正方形，
∴最底层有5个正方体，
A．由主视图和左视图可得第二层有2个正方体，第3层有1个正方体，故共有5+2+1=8个正方体，不可能是这种情况，符合题意；
B．由主视图和左视图可得第二层有4个正方体，第3层有2个正方体，故共有5+4+2=11个正方体，可能是这种情况，不符合题意；
C．由主视图和左视图可得第二层有4个正方体，第3层有1个正方体，故共有5+4+1=10个正方体，可能是这种情况，不符合题意；
D．由主视图和左视图可得第二层有4个正方体，第3层有2个正方体，故共有5+4+1=10个正方体，可能是这种情况，不符合题意；
故选A．

点评 本题考查由三视图判断几何体，解题的关键是明确俯视图中正方形的个数是组合几何体最底层正方体的个数，注意题目中组成组合几何体的正方体的个数应大于8．