题目内容
18.解下列方程:(1)x2-4x=1
(2)x(x+2)=5x+10
(3)(x+1)2-9=0
(4)(x+3)(x-1)=5.
分析 (1)直接利用配方法求出方程的根即可;
(2)利用提取公因式法分解因式解方程即可;
(3)利用直接开平方法解方程;
(4)首先去括号,合并同类项,进而利用十字相乘法分解因式解方程.
解答 解:(1)x2-4x=1,
(x-2)2=5,
则x-2=±$\sqrt{5}$,
解得:x1=2+$\sqrt{5}$,x2=2-$\sqrt{5}$;
(2)x(x+2)=5x+10,
x(x+2)-5(x+2)=0,
(x+2)(x-5)=0,
解得:x1=-2,x2=5;
(3)(x+1)2-9=0,
(x+1)2=9,
(x+1)=±3,
解得:x1=-4,x2=2;
(4)(x+3)(x-1)=5,
x2+2x-3=5,
x2+2x-8=0,
(x+4)(x-2)=0,
解得:x1=-4,x2=2.
点评 此题主要考查了配方法以及因式分解法解方程,正确分解因式是解题关键.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
8.有下列命题,其中正确的个数有( )
①三角形的内心到三个顶点距离相等;
②如果两条弧相等,那么它们所对的圆心角也相等
③垂直于弦的直径平分弦
④等腰三角形的边长是方程x2-6x+8=0的解,则这个等腰三角形的周长是10.
⑤平分弦的直径垂直于弦,并且平分弦所对的两条弧.
①三角形的内心到三个顶点距离相等;
②如果两条弧相等,那么它们所对的圆心角也相等
③垂直于弦的直径平分弦
④等腰三角形的边长是方程x2-6x+8=0的解,则这个等腰三角形的周长是10.
⑤平分弦的直径垂直于弦,并且平分弦所对的两条弧.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
6.无论k取任何实数,直线y=kx-3k+2上总有一个定点到原点的距离不变,这个距离为( )
| A. | $\sqrt{3}$ | B. | $\sqrt{13}$ | C. | $\sqrt{10}$ | D. | $2\sqrt{2}$ |
3.下列各组中的两个代数式为同类项的是( )
| A. | 3m2n与-m2n3 | B. | $\frac{1}{2}xy$与22yx | C. | 53与a3 | D. | 23x与2x3 |
7.下列运算正确的是( )
| A. | 992=(100-1)2=1002-1 | B. | 3a+2b=5ab | ||
| C. | $\sqrt{9}$=±3 | D. | x7÷x5=x2 |
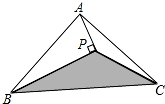 如图,△ABC的面积为1cm2,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为0.5cm2.
如图,△ABC的面积为1cm2,BP平分∠ABC,AP⊥BP于P,则△PBC的面积为0.5cm2.