题目内容
2.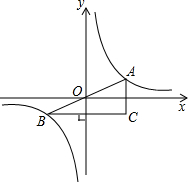 如图,A,B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴,则△ABC的面积为2.
如图,A,B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴,则△ABC的面积为2.
分析 设A点坐标为(x、$\frac{1}{x}$),根据A、B两点关于原点对称可知,B点坐标为(-x,-$\frac{1}{x}$),可求出C点坐标,利用矩形的面积公式可求出矩形OECD的面积,再根据反比例函数中系数k的几何意义可求出△AOE与△BOD的面积,把矩形OECD的面积与两三角形的面积相加即可得出结论.
解答 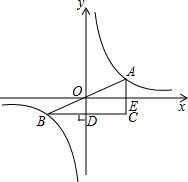 解:如图所示,
解:如图所示,
设A点坐标为(x、$\frac{1}{x}$),则B点坐标为(-x,-$\frac{1}{x}$),
∴C点坐标为(x,-$\frac{1}{x}$),
∴S矩形OECD=x•|-$\frac{1}{x}$|=1,
∵A、B为函数y=$\frac{1}{x}$图象上两点,
∴S△AOE=S△BOD=$\frac{1}{2}$k=$\frac{1}{2}$,
∴S△ABC=S矩形OECD+S△AOE+S△BOD=1+$\frac{1}{2}$+$\frac{1}{2}$=2,
故答案为:2.
点评 本题考查的是反比例函数中系数k的几何意义,根据A、B两点关于原点对称求出C点坐标,进而求出四边形OECD的面积是解答此题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
12.4的平方根是( )
| A. | ±2 | B. | 2 | C. | -2 | D. | ±$\sqrt{2}$ |
17.正比例函数y=(2k+1)x,若y随x增大而减小,则k的取值范围是( )
| A. | k>-$\frac{1}{2}$ | B. | k<-$\frac{1}{2}$ | C. | k=$\frac{1}{2}$ | D. | k=0 |
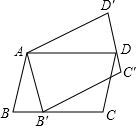 如图,将?ABCD绕点A逆时针旋转30°得到?AB′C′D′,点B′恰好落在BC边上,则∠DAB′=75°.
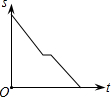
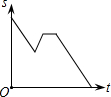
如图,将?ABCD绕点A逆时针旋转30°得到?AB′C′D′,点B′恰好落在BC边上,则∠DAB′=75°.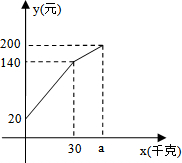 一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.
一农民带上若干千克自产的西红柿进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售,售出的西红柿千克数x与他手中持有的钱数y(含备用零钱)的关系,如图所示,结合图象回答下列问题.