题目内容
10.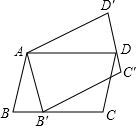 如图,将?ABCD绕点A逆时针旋转30°得到?AB′C′D′,点B′恰好落在BC边上,则∠DAB′=75°.
如图,将?ABCD绕点A逆时针旋转30°得到?AB′C′D′,点B′恰好落在BC边上,则∠DAB′=75°.
分析 根据旋转的性质得出AB=AB′,∠BAB′=30°,进而得出∠B的度数,再利用平行四边形的性质得出答案即可.
解答 解:∵平行四边形ABCD绕点A逆时针旋转30°,得到平行四边形AB′C′D′(点B′与点B是对应点,点C′与点C是对应点,点D′与点D是对应点),
∴AB=AB′,∠BAB′=30°,
∴∠B=∠AB′B=(180°-30°)÷2=75°,
∴∠DAB′=75°.
故答案为:75.
点评 此题主要考查了旋转的性质以及平行四边形的性质,根据已知得出∠B=∠AB′B=75°是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.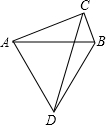 如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
 如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )
如图,以线段AB为边分别作直角三角形ABC和等边三角形ABD,其中∠ACB=90°.连接CD,当CD的长度最大时,此时∠CAB的大小是( )| A. | 75° | B. | 45° | C. | 30° | D. | 15° |
15.五边形的内角和是( )
| A. | 180° | B. | 360° | C. | 540° | D. | 720° |
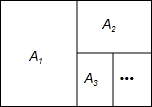 如图,An系列矩形纸张的规格特征是:①各矩形纸张都相似;②A1纸对裁后可以得到两张A2纸,A2纸对裁后可以得到两张A3纸,…,An纸对裁后可以得到两张An+1纸.
如图,An系列矩形纸张的规格特征是:①各矩形纸张都相似;②A1纸对裁后可以得到两张A2纸,A2纸对裁后可以得到两张A3纸,…,An纸对裁后可以得到两张An+1纸.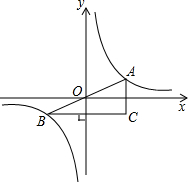 如图,A,B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴,则△ABC的面积为2.
如图,A,B是函数y=$\frac{1}{x}$的图象上关于原点O对称的任意两点,AC平行于y轴,BC平行于x轴,则△ABC的面积为2.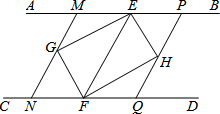 如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.
如图,AB∥CD,点E、F分别在AB、CD上,连接EF,∠AEF、∠CFE的平分线交于点G,∠BEF、∠DFE的平分线交于点H.