Question

1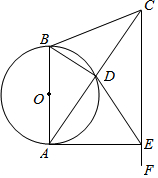．如图，在△ABC中，AB=CB，以AB为直径的⊙O交AC于点D．过点C作CF∥AB，在CF上取一点E，AE恰为⊙O的切线．
（1）试说明：△CBA∽△CDE；
（2）若AB=3，BD=2，求AE的长．

Answer 1

分析 （1）欲证明△CBA∽△CDE，只要证明∠DCE=∠DEC=∠BAC=∠BCA即可．
（2）由△ABC∽△EDC，推出$\frac{BC}{CD}$=$\frac{AC}{EC}$，求出EC，在Rt△ACE中，根据AE=$\sqrt{A{C}^{2}-E{C}^{2}}$计算即可．

解答 证明：（1）∵AB是直径，
∴∠ADB=90°，
∴BD⊥AC，∵BA=BC，
∴AD=DC，∠BCA=∠BAC，
∵AE是切线，
∴AE⊥AB，
∵CF∥AB，
∴AE⊥EC，∠BAC=∠ACE，
∴∠AEC=90°，
∴DE=DC，
∴∠DCE=∠DEC=∠BAC=∠BCA，
∴△BAC∽△DEC．

（2）在Rt△ABD中，∵AB=3，BD=2，
∴AD=DC=$\sqrt{A{B}^{2}-B{D}^{2}}$=$\sqrt{{3}^{2}-{2}^{2}}$=$\sqrt{5}$，
∴AC=2$\sqrt{5}$，
∵△ABC∽△EDC，
∴$\frac{BC}{CD}$=$\frac{AC}{EC}$，
∴$\frac{3}{\sqrt{5}}$=$\frac{2\sqrt{5}}{EC}$，
∴EC=$\frac{10}{3}$，
在Rt△ACE中，AE=$\sqrt{A{C}^{2}-E{C}^{2}}$=$\sqrt{（2\sqrt{5}）^{2}-（\frac{10}{3}）^{2}}$=$\frac{4}{3}$$\sqrt{5}$．

点评 本题考查了切线的判定、等腰三角形的性质、平行线的性质、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识，属于中考常考题型．