题目内容
9.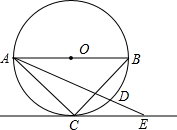 已知AB为⊙O的直径,$\widehat{BD}$=2$\widehat{CD}$,CE∥AB切⊙O于C点,交AD延长线于E点,若⊙O半径为2cm,求AE的长.
已知AB为⊙O的直径,$\widehat{BD}$=2$\widehat{CD}$,CE∥AB切⊙O于C点,交AD延长线于E点,若⊙O半径为2cm,求AE的长.
分析 利用切线的性质得出CO⊥CE,进而得出∠AEF=30°,AF=2cm,即可得出答案.
解答 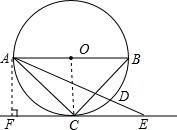 解:连接CO,过点A作AF⊥EC延长线于点F,
解:连接CO,过点A作AF⊥EC延长线于点F,
∵CE∥AB切⊙O于C点,
∴CO⊥CE,∠BOC=90°,
∴∠BAC=90°,则∠BAC=45°,
∵$\widehat{BD}$=2$\widehat{CD}$,
∴∠BAD=30°,
∵CE∥AB,
∴∠AEC=30°,AF=CO=2cm,
∴AE=2AF=4cm.
点评 此题主要考查了切线的性质以及平行线的性质,得出∠AEF=30°是解题关键.

练习册系列答案
相关题目
19.以下列各组线段长为边,能组成三角形的是( )
| A. | 1cm,2cm,3cm | B. | 4cm,6cm,8cm | C. | 12cm,5cm,6cm | D. | 2cm,3cm,6cm |
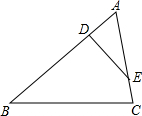 如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )
如图,D,E分别是△ABC的边AB,AC上的点,$\frac{BD}{AD}$=$\frac{AE}{CE}$=3,且∠AED=∠B,则△AED与△ABC的面积比是( )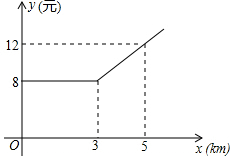 某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km.
某市出租车计费方法如图所示,x(km)表示行驶里程,y(元)表示车费,若某乘客有一次乘出租车的车费为42元,则这位乘客乘车的里程为20km. 如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1
如图,在平行四边形ABCD中,对角线AC、BD交于点O,M为AD中点,连接CM交BD于点N,且ON=1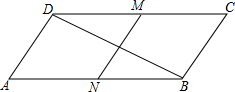 已知:平行四边形ABCD,AB=2AD,∠A=60°,M,N分别是DC,AB中点.求证:MN⊥DB.
已知:平行四边形ABCD,AB=2AD,∠A=60°,M,N分别是DC,AB中点.求证:MN⊥DB.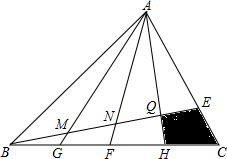 如图,设△ABC的面积为10cm2,若CE=$\frac{1}{4}$AC,BG=GF=FH=HC,求阴影四边形的面积.
如图,设△ABC的面积为10cm2,若CE=$\frac{1}{4}$AC,BG=GF=FH=HC,求阴影四边形的面积.