若x=$\frac{1}{2-\sqrt{3}}$.y=$\frac{1}{2+\sqrt{3}}$.则x2-xy+y2=13．题目和参考答案——青夏教育精英家教网—

题目内容

12．若x=$\frac{1}{2-\sqrt{3}}$，y=$\frac{1}{2+\sqrt{3}}$，则x²-xy+y²=13．

分析先将x与y分母有理化，然后利用配方法即可化简求值．

解答解：∵x=$\frac{1}{2-\sqrt{3}}$，y=$\frac{1}{2+\sqrt{3}}$，
∴x=2+$\sqrt{3}$，y=2-$\sqrt{3}$，
∴x+y=4，xy=4-3=1，
∴原式=（x+y）²-3xy
=16-3
=13
故答案：13

点评本题考查分母有理化，解题的关键是求出x+y与xy的值，本题属于基础题型．

练习册系列答案

相关题目

2．关于x的一元二次方程x²-x+k=0有两个实数根，则k的取值范围是（　　）

3．“黄金1号”玉米种子的价格为5元/千克，如果一次购买2千克以上的种子，超过2千克部分的种子价格打6折，设购买种子数量为x千克，付款金额为y元，则y与x的函数关系的图象大致是（　　）

20．已知有理数a，b满足|a+1|+（b-2017）²=0，那么ab=-2017．

7．下列一元二次方程，无实数解的是（　　）

0.5=$\sqrt{（0.5）^{2}}$

B．

3=（$\sqrt{3}$）²

C．

-$\sqrt{（-0.3）^{2}}$=-0.3

D．

（5$\sqrt{7}$）²=35

4．如图，在Rt△ABC中，∠C=90°，AC=6，M、N分别是边AB、AC的中点，在射线MN上取点D，使∠ADM=∠BAC，连接AD．
（1）如图1，当BC=3时，求DM的长．
（2）如图2，以AB为底边在AB的左侧作等腰△ABE，并且使顶角∠AEB=2∠BAC，连接EM．
①判断四边形AEMD的形状，并说明理由．
②设BC=x（x＞0），四边形AEMD的面积为y，试用含x的式子表示y，并说明是否存在x的值，使得四边形AEMD的面积等于△ABC的面积？若存在，请求出x的值；若不存在，请说明理由．

1．点A，B，P在同一直线上，下列说法正确的是（　　）

	A．	若AB=2PA，则P是AB的中点		B．	若AP=PB=$\frac{1}{2}$AB，则P是AB的中点
	C．	若AB=2PB，则P是AB的中点		D．	若AB=PB=$\frac{1}{2}$PA，则P是AB的中点

2．

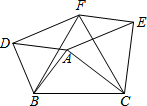如图，在△ABC中，AB=5，AC=12，BC=13，△ABD、△ACE、△BCF都是等边三角形，则四边形AEFD的面积S=30．

试题分类