题目内容
11.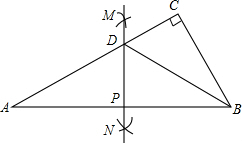 如图,△ABC中,∠C=90°,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.若DC=3,BC=4,则AB=4$\sqrt{5}$.
如图,△ABC中,∠C=90°,分别以顶点A、B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧在直线AB两侧分别交于M、N两点,过M、N作直线交AB于点P,交AC于点D,连接BD.若DC=3,BC=4,则AB=4$\sqrt{5}$.
分析 由题意MN垂直平分线段AB,可得BD=AD,在Rt△BCD中,可得BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,推出AD=BD=5,AC=AD+DC=8,在Rt△ACB中,根据AB=$\sqrt{A{C}^{2}+B{C}^{2}}$即可解决问题.
解答 解:由题意MN垂直平分线段AB,
∴BD=AD,
在Rt△BCD中,BD=$\sqrt{C{D}^{2}+B{C}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴AD=BD=5,AC=AD+DC=8,
在Rt△ACB中,AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{4}^{2}}$=4$\sqrt{5}$,
故答案为4$\sqrt{5}$.
点评 本题考查作图-基本作图、线段的垂直平分线的性质、勾股定理等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.

练习册系列答案
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
1.点A,B,P在同一直线上,下列说法正确的是( )
| A. | 若AB=2PA,则P是AB的中点 | B. | 若AP=PB=$\frac{1}{2}$AB,则P是AB的中点 | ||
| C. | 若AB=2PB,则P是AB的中点 | D. | 若AB=PB=$\frac{1}{2}$PA,则P是AB的中点 |
16.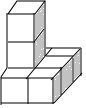 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )| A. | 正视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |
1.在一个不透明的口袋里有红、黄、蓝三种颜色的小球,这些球除颜色外完全相同,其中有5个黄球,4个蓝球.若随机摸出一个蓝球的概率为$\frac{1}{3}$,则随机摸出一个红球的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{3}$ | C. | $\frac{5}{12}$ | D. | $\frac{1}{2}$ |
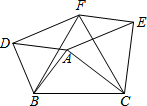 如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.
如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.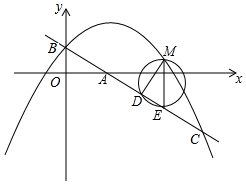 在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).
在平面直角坐标系中,直线y=-$\frac{3}{4}$x+1交y轴于点B,交x轴于点A,抛物线y=-$\frac{1}{2}$x2+bx+c经过点B,与直线y=-$\frac{3}{4}$x+1交于点C(4,-2).