题目内容
7.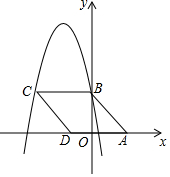 如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=-x2-5x+c经过点B、C,则菱形ABCD的面积为20.
如图,在平面直角坐标系中,菱形ABCD的顶点A的坐标为(3,0),顶点B在y轴正半轴上,顶点D在x轴负半轴上.若抛物线y=-x2-5x+c经过点B、C,则菱形ABCD的面积为20.
分析 根据抛物线的解析式结合抛物线过点B、C,即可得出点C的横坐标,由菱形的性质可得出AD=AB=BC=5,再根据勾股定理可求出OB的长度,套用平行四边形的面积公式即可得出菱形ABCD的面积.
解答 解:抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{5}{2}$.
∵抛物线y=-x2-5x+c经过点B、C,且点B在y轴上,BC∥x轴,
∴点C的横坐标为-5.
∵四边形ABCD为菱形,
∴AB=BC=AD=5,
∴点D的坐标为(-2,0),OA=3.
在Rt△ABC中,AB=5,OA=3,
∴OB=$\sqrt{A{B}^{2}-O{A}^{2}}$=4,
∴S菱形ABCD=AD•OB=5×4=20.
故答案为:20.
点评 本题考查了二次函数图象上点的坐标特征、二次函数的性质、菱形的性质以及平行四边形的面积,根据二次函数的性质、菱形的性质结合勾股定理求出AD=5、OB=4是解题的关键.

练习册系列答案
相关题目
17.下列式子不成立的是( )
| A. | 0.5=$\sqrt{(0.5)^{2}}$ | B. | 3=($\sqrt{3}$)2 | C. | -$\sqrt{(-0.3)^{2}}$=-0.3 | D. | (5$\sqrt{7}$)2=35 |
12.若a-b=-7,ab=-2,则a2b3-a3b2=( )
| A. | -89 | B. | -28 | C. | 89 | D. | 28 |
16.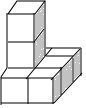 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
 如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )
如图,由8个大小相同的正方体搭成的几何体,则关于它的视图说法正确的是( )| A. | 正视图的面积最大 | B. | 左视图的面积最大 | ||
| C. | 俯视图的面积最大 | D. | 三个视图的面积一样大 |
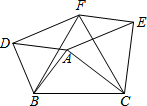 如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.
如图,在△ABC中,AB=5,AC=12,BC=13,△ABD、△ACE、△BCF都是等边三角形,则四边形AEFD的面积S=30.