Question

13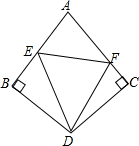．如图，BD=CD，∠ABD=∠ACD=90°，点E，F分别在AB，AC上，若ED平分∠BEF
（1）求证：FD平分∠EFC；
（2）求证：EF=BE+CF．

Answer 1

分析 （1）过D作DM⊥EF，根据角平分线的性质可得BD=DM，然后可得DC=DM，再根据到角两边距离相等的点在角的平分线上可得FD平分∠EFC；
（2）首先证明△BDE≌△MDE可得EB=EM，同理可得CF=MF，进而可得EF=BE+CF．

解答 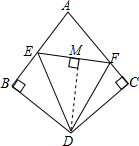证明：（1）过D作DM⊥EF，
∵ED平分∠BEF，
∴BD=DM，
∵BD=CD，
∴DC=DM，
∴FD平分∠EFC；

（2）∵ED平分∠BEF，
∴∠BDE=∠MDE，
在△BDE和△MDE中$\left\{\begin{array}{l}{BD=DM}\\{∠BDE=∠MDE}\\{ED=ED}\end{array}\right.$，
∴△BDE≌△MDE（SAS），
∴EB=EM，
同理CF=MF，
∴EF=BE+CF．

点评 此题主要考查了全等三角形的判定和性质，以及角平分线的性质和判定，关键是掌握全等三角形的判定方法，掌握到角两边距离相等的点在角的平分线上．