题目内容
17. 如图,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.
如图,网格中的每个小正方形的边长均为1,点A、B在小正方形的顶点上.(1)在图中确定点C(点C在小正方形的顶点上),使△ABC是以AB为斜边的直角三角形,AC<BC,画出△ABC;
(2)将(1)中所画△ABC绕点B顺时针旋转90°得到△A′BC′(点A′,C′分别为点A、C的对应点),画出△A′BC′,直接写出点A经过旋转到点A′所经过的路线长为$\frac{5}{2}$π.
分析 (1)以AB为直径作圆,圆与方格网格点的交点即为所求;
(2)分别作出△ABC三顶点绕点B顺时针旋转90°得到对应点,顺次连接即可得,由弧长公式可得路线长.
解答 解:(1)如图,点C即为所求;
(2)如图,△A′BC′即为所求三角形,
∵AB=5,∠ABA′=90°,
∴点A经过旋转到点A′所经过的路线长为$\frac{90•π•5}{180}$=$\frac{5}{2}$π,
故答案为:$\frac{5}{2}$π.
点评 本题主要考查作图-旋转作图、圆周角定理及弧长公式,熟练掌握圆周角定理及旋转变换的定义及性质是解题的关键.

练习册系列答案
相关题目
9.已知$\sqrt{x+y-1}$+$\sqrt{x-y+3}$=0,则(x+y)2016=( )
| A. | 22016 | B. | -1 | C. | 1 | D. | -22016 |
 如图所示,四边形ABCD为平行四边形,CE平分∠BCD,交AB边于点E,若AD=6,AB=8,则线段AE的长为2.
如图所示,四边形ABCD为平行四边形,CE平分∠BCD,交AB边于点E,若AD=6,AB=8,则线段AE的长为2.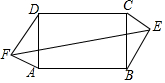 如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于$\sqrt{394}$.
如图,在矩形ABCD中,AD=5,AB=15,E、F分别为矩形外两点,DF=BE=4,AF=CE=3,则EF等于$\sqrt{394}$.
 如图的几何体是由四个大小相同的小正方体拼成,则这个几何体的左视图是( )
如图的几何体是由四个大小相同的小正方体拼成,则这个几何体的左视图是( )


