题目内容
5.在平面直角坐标系中,点P′是由点P(2,3)先向左平移3个单位,再向下平移2个单位得到的,则点P′的坐标是( )| A. | (5,1) | B. | (-1,1) | C. | (5,5) | D. | (-1,5) |
分析 让点P的横坐标减3,纵坐标减2即可得到平移后点P′的坐标.
解答 解:点P′的横坐标为2-3=-1,纵坐标为3-2=1,
所以点P′的坐标是(-1,1),
故选B.
点评 本题考查了坐标与图形变化-平移,用到的知识点为:点的平移,左右平移只改变点的横坐标,左减右加;上下平移只改变点的纵坐标,上加下减.

练习册系列答案
相关题目
16.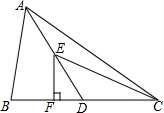 在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
 在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )
在△ABC中,AD是BC边上的中线,点E是AD中点,过点E作垂线交BC于点F,已知BC=10,△ABD的面积为12,则EF的长为( )| A. | 1.2 | B. | 2.4 | C. | 3.6 | D. | 4.8 |
20.对于二次函数y=2x2-8x+6的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 与x轴的交点横坐标是x1=-1,x2=-3 | ||
| C. | 对称轴是直线x=-2 | D. | 由y=-2(x-2)2+2的图象轴对称得到 |
10.把抛物线y=2x2向左平移3个单位,再向上平移2个单位所得抛物线的解析式为( )
| A. | y=2(x+3)2+2 | B. | y=2(x-2)2+3 | C. | y=2(x+2)2+3 | D. | y=2(x-3)2+2 |
17. 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
 如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )
如图,Rt△ABC中,∠ACB=90°,CD⊥AB于点D,下列结论中错误的是( )| A. | AC2=AD•AB | B. | CD2=CA•CB | C. | CD2=AD•DB | D. | BC2=BD•BA |
14.在平面直角坐标系中,已知点A(3,3),在坐标轴上确定点B,使△AOB为等腰三角形,则符合条件的点B共有( )
| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
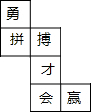 水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图,是一个正方体的平面展开图,若图中的“才”表示正方体的前面,“拼”表示正方体的左面,“会”表示上面,则“勇”“搏”分别表示正方体的后面、下面.
水平放置的正方体的六个面分别用“前面、后面、上面、下面、左面、右面”表示,如图,是一个正方体的平面展开图,若图中的“才”表示正方体的前面,“拼”表示正方体的左面,“会”表示上面,则“勇”“搏”分别表示正方体的后面、下面. 实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入$\frac{5}{3}$或$\frac{20}{3}$分钟水量后,甲的水位比乙高1cm.
实验室里,水平桌面上有甲、乙、丙三个相 同高度的圆柱形容器(容器足够高),底面半径之比为1:2:1,用两个相同的管子在10cm高度处连通(即管子底部离容器底10cm),现三个容器中,只有乙中有水,水位高4cm,如图所示.若每分钟同时向甲和丙注入相同量的水,开始注水1分钟,甲的水位上升3cm.则开始注入$\frac{5}{3}$或$\frac{20}{3}$分钟水量后,甲的水位比乙高1cm.