题目内容
14.在平面直角坐标系中,已知点A(3,3),在坐标轴上确定点B,使△AOB为等腰三角形,则符合条件的点B共有( )| A. | 5个 | B. | 6个 | C. | 7个 | D. | 8个 |
分析 题中没有指明AO,BO,AB是底还是腰,故应该分情况进行分析,注意不但要考虑到AO,BO,AB是底还是腰,而且要考虑A,B是在正半轴还是在负半轴.
解答 解:(1)当AO,BO为腰时,
①当AO=BO(B在Y轴正半轴上),
∵点A坐标为(3,3),O为坐标原点,
∴OA=OB=3$\sqrt{2}$,
∴B1=(0,3$\sqrt{2}$),
②当AO=BO(B在Y轴负半轴上),
同理:B2=(0,-3$\sqrt{2}$).
③当AO=BO(B在X轴正半轴上),
同理:B3=(3$\sqrt{2}$,0).
④当AO=BO(B在X轴负半轴上),
同理:B4=(-$3\sqrt{2}$,0).
(2)当AO为底时,
⑤AB=BO(B在Y轴正半轴上),
同理:B7=(0,3).
⑥当AB=BO(B在X轴正半轴上),
同理:B8=(3,0).
故选B.
点评 此题主要考查等腰三角形的性质及坐标与图形性质的综合运用,注意分类讨论思想的运用.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
4.现有2cm,4cm,5cm,8cm,9cm长的五根木棒,任意选取三根组成一个三角形,选法种数有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |
5.在平面直角坐标系中,点P′是由点P(2,3)先向左平移3个单位,再向下平移2个单位得到的,则点P′的坐标是( )
| A. | (5,1) | B. | (-1,1) | C. | (5,5) | D. | (-1,5) |
9.已知一次函数y=2x+3,则当自变量x减小a时,函数y的变化情况是( )
| A. | 增大2a | B. | 减小2a | C. | 增大a | D. | 减小a |
3.如果3x2n-1ym与-5xmy-3是同类项,则mn( )
| A. | -3 | B. | -4 | C. | 3 | D. | 4 |
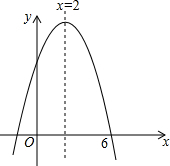 二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=2,若此抛物线与x轴的一个交点为(6,0),则抛物线与x轴的另一个交点坐标是(-2,0).
二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=2,若此抛物线与x轴的一个交点为(6,0),则抛物线与x轴的另一个交点坐标是(-2,0).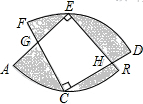 如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.
如图,两个半径相等的直角扇形的圆心分别在对方的圆弧上,半径AE、CF交于点G,半径BE、CD交于点H,且C是$\widehat{AB}$的中点,若扇形的半径为4,则图中四边形EGCH的面积为8平方单位.