题目内容
17．
如图，Rt△ABC中，∠ACB=90°，CD⊥AB于点D，下列结论中错误的是（ ）| A． | AC2=AD•AB | B． | CD2=CA•CB | C． | CD2=AD•DB | D． | BC2=BD•BA |
分析 直接根据射影定理对各选项进行判断．
解答 解：∵∠ACB=90°，CD⊥AB于点D，
∴AC2=AD•AB，CD2=DA•DB，BC2=BD•BA．
故选B．
点评 本题考查了射影定理：直角三角形中，斜边上的高是两直角边在斜边上射影的比例中项；每一条直角边是这条直角边在斜边上的射影和斜边的比例中项．
练习册系列答案
全优点练单元计划系列答案
相关题目
5．在平面直角坐标系中，点P′是由点P（2，3）先向左平移3个单位，再向下平移2个单位得到的，则点P′的坐标是（ ）
| A． | （5，1） | B． | （-1，1） | C． | （5，5） | D． | （-1，5） |
12．
如图，点A，B，C是⊙O上的三点，∠AOC=110°，则∠ABC等于（ ）
如图，点A，B，C是⊙O上的三点，∠AOC=110°，则∠ABC等于（ ）| A． | 70° | B． | 65° | C． | 55° | D． | 50° |
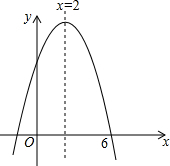二次函数y=ax2+bx+c的图象如图所示，对称轴为直线x=2，若此抛物线与x轴的一个交点为（6，0），则抛物线与x轴的另一个交点坐标是（-2，0）．
9．已知一次函数y=2x+3，则当自变量x减小a时，函数y的变化情况是（ ）
| A． | 增大2a | B． | 减小2a | C． | 增大a | D． | 减小a |
