题目内容
4.计算(1)(-2)-1+(-$\frac{1}{2}$)-3+(-$\frac{1}{2}$)0
(2)(-$\frac{1}{3}$ax4y3)2÷(-$\frac{1}{18}$ax2y)•8a2y
(3)(2a+3b-c)(2a-3b+c)
(4)[(3x-2)2-2(x+2)(x+1)]÷(-2x)
分析 (1)先算负整数指数幂和0指数幂,再算加法即可;
(2)先算积的乘方,再算同底数幂乘除;
(3)先利用平方差公式,再利用完全平方公式计算;
(4)先利用完全平方公式和整式的乘法计算,再进一步合并,最后算除法.
解答 解:(1)原式=-$\frac{1}{2}$-8+1
=-7$\frac{1}{2}$;
(2)原式=$\frac{1}{9}$a2x8y6÷(-$\frac{1}{18}$ax2y)•8a2y
=-16a3x8y6;
(3)原式=(2a)2-(3b-c)2
=4a2-9b2+6bc-c2;
(4)原式=[9x2-12x+4-2x2-6x-4]÷(-2x)
=[7x2-18x]÷(-2x)
=-3.5x+9.
点评 此题考查整式的混合运算,掌握运算顺序与计算的方法是解决问题的关键.

练习册系列答案
相关题目
12.我国雾霾天气多发,PM2.5颗粒物被称为大气的元凶,PM2.5是指直径小于或等于2.5微米的颗粒物,已知1毫米=1000微米,用科学记数法表示2.5微米是( )
| A. | 2.5×10-6m | B. | 25×10-6m | C. | 2.5×10-5m | D. | 25×10-5m |
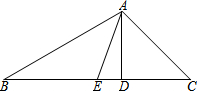 如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,∠B=30°,求tan∠DAE的值.
如图,在△ABC中,AD是BC边上的高,AE是BC边上的中线,∠C=45°,∠B=30°,求tan∠DAE的值. 已知P为正方形ABCD的对角线AC上任意一点,求证:PB=PD.
已知P为正方形ABCD的对角线AC上任意一点,求证:PB=PD.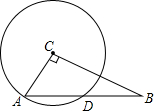 如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.