题目内容
17.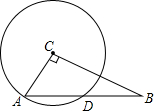 如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.
如图,在Rt△ABC中,∠ACB=90°,AB=10,以点C为圆心,CA为半径的圆与AB交于点D,$sinB=\frac{3}{5}$.(1)求⊙C的半径r;
(2)求弦AD的长.
分析 (1)在Rt△ACB中利用∠B的正弦可计算出AC的长;
(2)作CH⊥AD于H,如图,则根据垂径定理得到AH=DH,再根据等角的余角相等得到∠B=∠ACH,则在Rt△ACH中,利用∠ACH的正弦可计算出AH,从而得到AD的长.
解答 解:(1)在Rt△ACB中,∵sinB=$\frac{AC}{AB}$=$\frac{3}{5}$,
∴AC=$\frac{3}{5}$×10=6,
即⊙C的半径r=6;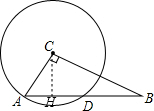 (2)作CH⊥AD于H,如图,则AH=DH,
(2)作CH⊥AD于H,如图,则AH=DH,
∵∠A+∠B=90°,∠A+∠ACH=90°,
∴∠B=∠ACH,
在Rt△ACH中,∵sin∠ACH=$\frac{AH}{AC}$=$\frac{3}{5}$,
∴AH=$\frac{3}{5}$×6=$\frac{18}{5}$,
∴AD=2AH=$\frac{36}{5}$.
点评 本题考查了垂径定理:垂直于弦的直径平分这条弦,并且平分弦所对的两条弧.也考查了解直角三角形.

练习册系列答案
相关题目
2. 如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
 如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )
如图:△ABC中,DE∥BC,AD=5,BD=10,AE=3.则AC的值为( )| A. | 9 | B. | 6 | C. | 3 | D. | 4 |
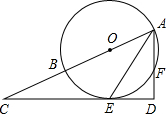 如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.
如图,AB为⊙O的直径,AE平分∠BAF,交⊙O于点E,过点E作直线ED⊥AF,交AF的延长线于点D,交AB的延长线于点C.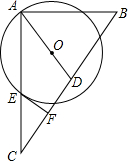 如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)
如图,在△ABC中,∠BAC=90°,D为BC上的中点,O是线段AD上一点,以点O为圆心,OA长为半径的⊙O交AC于点E,EF⊥BC于点F,则EF是⊙O的切线.(填“是”或“不是”)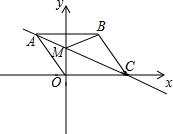 已知:如图平面直角坐标系xOy中,C在x轴上,四边形OABC为菱形,且A点坐标
已知:如图平面直角坐标系xOy中,C在x轴上,四边形OABC为菱形,且A点坐标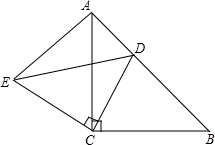 已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,求∠EAC的度数.
已知:如图,△ABC和△ECD都是等腰直角三角形,∠ACB=∠DCE=90°,D为AB边上一点,求∠EAC的度数.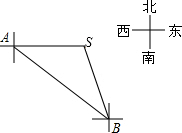 为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)
为维护南海主权,我海军舰艇加强对南海海域的巡航,2015年4月10日上午9时,我海巡001号舰艇在观察点A处观测到其正东方向80$\sqrt{2}$海里处有一灯塔S,该舰艇沿南偏东45°的方向航行,11时到达观察点B,测得灯塔S位于其北偏西15°方向,求该舰艇的巡航速度?(结果保留整数)