题目内容
2.用因式分解法解下列方程:(1)5x2-4x=0;
(2)3x(2x+1)=4x+2;
(3)(2x-1)2-3(2x-1)=4.
分析 (1)利用因式分解法解方程;
(2)先变形得到3x(2x+1)-2(2x+1)=0,然后利用因式分解法解方程;
(3)先移项得到(2x-1)2-3(2x-1)-4=0,然后把方程看作关于2x-1的一元二次方程,再利用因式分解法解方程.
解答 解:(1)x(5x-4)=0,
x=0或5x-4=0,
所以x1=0,x2=$\frac{4}{5}$;
(2)3x(2x+1)-2(2x+1)=0,
(2x+1)(3x-2)=0,
2x+1=0或3x-2=0,
所以x1=-$\frac{1}{2}$,x2=$\frac{2}{3}$;
(3)(2x-1)2-3(2x-1)-4=0,
(2x-1-4)(2x-1+1)=0,
2x-1-4=0或2x-1+1=0,
所以x1=$\frac{5}{2}$,x2=0.
点评 本题考查了解一元二次方程-因式分解法:先把方程的右边化为0,再把左边通过因式分解化为两个一次因式的积的形式,那么这两个因式的值就都有可能为0,这就能得到两个一元一次方程的解,这样也就把原方程进行了降次,把解一元二次方程转化为解一元一次方程的问题了(数学转化思想).

练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
10. 实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )
实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )
 实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )
实数a,b在数轴上对应的位置,如图所示:则|a-b|-|b|等于( )| A. | a | B. | a-2b | C. | -a | D. | b-a |
 如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点.
如图,已知反比例函数y=$\frac{k}{x}$的图象与一次函数y=ax+b的图象交于M(2,m)和N(-1,-4)两点. 如图所示,点P是△ABC的两条角平分线BP、CP的交点,若∠A=100°,求∠BPC的度数.
如图所示,点P是△ABC的两条角平分线BP、CP的交点,若∠A=100°,求∠BPC的度数.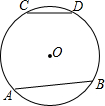 如图,已知A,B,C,D为圆O上的四点,且$\widehat{AB}$=2$\widehat{CD}$,请判断AB与2CD是否相等,说明理由.
如图,已知A,B,C,D为圆O上的四点,且$\widehat{AB}$=2$\widehat{CD}$,请判断AB与2CD是否相等,说明理由.