题目内容
方程x+
=2+
的解为x1=2,x2=
,方程x+
=3+
的解为x1=3,x2=
,方程x+
=4+
的解为x1=4,x2=
.根据以上规律,在解方程y+
=
时,可变形转化为:x+
=a+
的形式求解,并写出解题过程.
| 1 |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| x |
| 1 |
| 4 |
| 1 |
| 4 |
| y+2 |
| y+1 |
| 10 |
| 3 |
| 1 |
| x |
| 1 |
| a |
考点:分式方程的解
专题:
分析:根据已知材料可将方程y+
=
变形转化为y+1+
=3+
,所以其解为y1+1=3,y2+1=
,由此求出y1,y2的值.
| y+2 |
| y+1 |
| 10 |
| 3 |
| 1 |
| y+1 |
| 1 |
| 3 |
| 1 |
| 3 |
解答:解:∵方程y+
=
可变形转化为y+1+
=3+
,
∴y1+1=3,y2+1=
,
∴y1=2,y2=-
.
| y+2 |
| y+1 |
| 10 |
| 3 |
| 1 |
| y+1 |
| 1 |
| 3 |
∴y1+1=3,y2+1=
| 1 |
| 3 |
∴y1=2,y2=-
| 2 |
| 3 |
点评:本题考查了分式方程的解和解分式方程的应用,解此题的关键是找出材料中隐含的规律,通过做此题培养了学生的阅读能力和理解能力.

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
计算
的值为( )
| (-13)2 |
| A、169 | B、-13 |
| C、±13 | D、13 |
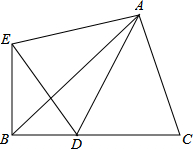 已知:在△ABC中,∠ABC=45°,点D是BC上一点,∠ADB=120°且CD=2BD,将△ADC沿着AD翻折,点C落在点E处.
已知:在△ABC中,∠ABC=45°,点D是BC上一点,∠ADB=120°且CD=2BD,将△ADC沿着AD翻折,点C落在点E处. 如图,BE、CD交于O点,OD=OE,∠B=∠C,△BOD和△COE全等吗?
如图,BE、CD交于O点,OD=OE,∠B=∠C,△BOD和△COE全等吗? 已知:AB∥CD,AD、BC相交于点O,且OA=OB.求证:
已知:AB∥CD,AD、BC相交于点O,且OA=OB.求证: 如图,点A(3,1)在直线y=-
如图,点A(3,1)在直线y=-