题目内容
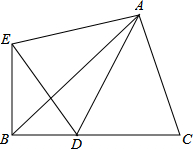 已知:在△ABC中,∠ABC=45°,点D是BC上一点,∠ADB=120°且CD=2BD,将△ADC沿着AD翻折,点C落在点E处.
已知:在△ABC中,∠ABC=45°,点D是BC上一点,∠ADB=120°且CD=2BD,将△ADC沿着AD翻折,点C落在点E处.(1)求证:BE⊥BC;
(2)求∠C的度数.
考点:翻折变换(折叠问题),角平分线的性质,等边三角形的判定与性质,直角三角形斜边上的中线
专题:
分析:(1)取DE的中点M,连接BM,如图1,根据邻补角的定义由∠ADB=120°得∠ADC=60°,再根据折叠的性质得DE=DC,∠ADE=∠ADC=60°,则∠BDE=60°,由于CD=2BD,则DE=2BD,DM=DB,原式可判断△BDM为等边三角形,得到EM=BM=MD,根据圆周角定理的推理得到△BDE为直角三角形,即BE⊥BC;
(2)作AF⊥BC于F,AG⊥DE于G,AH⊥BE于H,如图2,由∠ABC=45°,可判断四边形AFBH为正方形,根据正方形的性质得AF=AH,再根据角平分线的性质由DA平分∠EDC得到AF=AG,则可根据“HL”证明Rt△AHE≌Rt△AGE,Rt△ADG≌Rt△ADF,得到∠3=∠2,∠DAG=∠4,所以∠2+∠DAG=
∠FAH=45°,即∠DAE=45°,然后利用三角形内角和计算出∠1=75°,最后利用折叠的性质得到∠C=∠1=75°.
(2)作AF⊥BC于F,AG⊥DE于G,AH⊥BE于H,如图2,由∠ABC=45°,可判断四边形AFBH为正方形,根据正方形的性质得AF=AH,再根据角平分线的性质由DA平分∠EDC得到AF=AG,则可根据“HL”证明Rt△AHE≌Rt△AGE,Rt△ADG≌Rt△ADF,得到∠3=∠2,∠DAG=∠4,所以∠2+∠DAG=
| 1 |
| 2 |
解答:解:(1) 取DE的中点M,连接BM,如图1,
取DE的中点M,连接BM,如图1,
∵∠ADB=120°,
∴∠ADC=60°,
∵△ADC沿着AD翻折,点C落在点E处,
∴DE=DC,∠ADE=∠ADC=60°,
∴∠BDE=60°,
∵CD=2BD,
∴DE=2BD,
∴DM=DB,
∴△BDM为等边三角形,
∴BM=DM,
即EM=BM=MD,
∴△BDE为直角三角形,
∴BE⊥BC;
(2) 作AF⊥BC于F,AG⊥DE于G,AH⊥BE于H,如图2,
作AF⊥BC于F,AG⊥DE于G,AH⊥BE于H,如图2,
则四边形AFBH为矩形,
∵∠ABC=45°,
∴四边形AFBH为正方形,
∴AF=AH,
∵∠ADC=∠ADE,即DA平分∠EDC,
∴AF=AG,
在Rt△AHE和Rt△AGE中
,
∴Rt△AHE≌Rt△AGE(HL),
∴∠3=∠2,
同理可得Rt△ADG≌Rt△ADF,
∴∠DAG=∠4,
∴∠2+∠DAG=
∠FAH=45°,即∠DAE=45°,
∴∠1=180°-∠DAE-∠ADE=75°,
∵△ADC沿着AD翻折,点C落在点E处,
∴∠C=∠1=75°.
 取DE的中点M,连接BM,如图1,
取DE的中点M,连接BM,如图1,∵∠ADB=120°,
∴∠ADC=60°,
∵△ADC沿着AD翻折,点C落在点E处,
∴DE=DC,∠ADE=∠ADC=60°,
∴∠BDE=60°,
∵CD=2BD,
∴DE=2BD,
∴DM=DB,
∴△BDM为等边三角形,
∴BM=DM,
即EM=BM=MD,
∴△BDE为直角三角形,
∴BE⊥BC;
(2)
 作AF⊥BC于F,AG⊥DE于G,AH⊥BE于H,如图2,
作AF⊥BC于F,AG⊥DE于G,AH⊥BE于H,如图2,则四边形AFBH为矩形,
∵∠ABC=45°,
∴四边形AFBH为正方形,
∴AF=AH,
∵∠ADC=∠ADE,即DA平分∠EDC,
∴AF=AG,
在Rt△AHE和Rt△AGE中
|
∴Rt△AHE≌Rt△AGE(HL),
∴∠3=∠2,
同理可得Rt△ADG≌Rt△ADF,
∴∠DAG=∠4,
∴∠2+∠DAG=
| 1 |
| 2 |
∴∠1=180°-∠DAE-∠ADE=75°,
∵△ADC沿着AD翻折,点C落在点E处,
∴∠C=∠1=75°.
点评:本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了角平分线的性质、等边三角形的判定与性质和直角三角形的判定方法.

练习册系列答案
相关题目
-π、1、0、-
四个数中,最小的数是( )
| 3 |
| 4 |
| A、-π | ||
| B、1 | ||
| C、0 | ||
D、-
|
 如图的最小正方形的边长均为1,则阴影部分正方形的面积和边长分别是( )
如图的最小正方形的边长均为1,则阴影部分正方形的面积和边长分别是( )A、5和
| ||
B、8和
| ||
C、10和
| ||
D、2和
|
 如图,?ABCD中,E是AD的中点,△BCE是等边三角形.求证:四边形ABCD是矩形.
如图,?ABCD中,E是AD的中点,△BCE是等边三角形.求证:四边形ABCD是矩形.