题目内容
已知a是实数,且方程x2+2ax+1=0有两个不相等的实根,试判别方程x2+2ax+1-12(a2x2-a2-1)=0有无实根?
考点:根的判别式
专题:
分析:根据方程x2+2ax+1=0有两个不相等的实根,利用根的判别式求出a2>1,再利用根的判别式,求出△=576a4+580a2-52>0,从而判断出方程x2+2ax+1-12(a2x2-a2-1)=0一定有两个不相等的实根.
解答:解:∵方程x2+2ax+1=0有两个不相等的实根,
∴△=(2a)2-4>0,
∴a2>1,
∵方程x2+2ax+1-12(a2x2-a2-1)=0可化为(1-12a2)x2+2ax+(12a2+13)=0,
∴△=(2a)2-4(1-12a2)(12a2+13)=576a4+580a2-52>0,
∴方程x2+2ax+1-12(a2x2-a2-1)=0一定有两个不相等的实根.
∴△=(2a)2-4>0,
∴a2>1,
∵方程x2+2ax+1-12(a2x2-a2-1)=0可化为(1-12a2)x2+2ax+(12a2+13)=0,
∴△=(2a)2-4(1-12a2)(12a2+13)=576a4+580a2-52>0,
∴方程x2+2ax+1-12(a2x2-a2-1)=0一定有两个不相等的实根.
点评:本题考查了一元二次方程根的判别式,要知道,一元二次方程根的情况与判别式△的关系:
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.
(1)△>0?方程有两个不相等的实数根;
(2)△=0?方程有两个相等的实数根;
(3)△<0?方程没有实数根.

练习册系列答案
相关题目
点P(x-1,x+1),当x变化时,点P不可能在第( )象限.
| A、一 | B、二 | C、三 | D、四 |
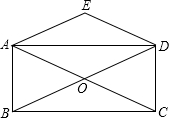 矩形ABCD的对角线AC,BD相交于点O,AE∥BD,DE∥AC.
矩形ABCD的对角线AC,BD相交于点O,AE∥BD,DE∥AC. 如图,点D、E在BC上,且AB=AC,AD=AE.
如图,点D、E在BC上,且AB=AC,AD=AE.