题目内容
14.计算:($\frac{1}{\sqrt{2}+1}$+$\frac{1}{\sqrt{3}+\sqrt{2}}$+$\frac{1}{\sqrt{4}+\sqrt{3}}$+…+$\frac{1}{\sqrt{2010}+\sqrt{2009}}$)($\sqrt{2010}$+1)分析 先进行分母有理化,然后合并求解.
解答 解:原式=[($\sqrt{2}$-1)+($\sqrt{3}$-$\sqrt{2}$)+($\sqrt{4}$-$\sqrt{3}$)+…($\sqrt{2010}$-$\sqrt{2009}$)]($\sqrt{2010}$+1)
=($\sqrt{2010}$-1)($\sqrt{2010}$+1)
=2010-1
=2009.
点评 本题考查了二次根式的混合运算,解答本题的关键是首先进行分母有理化,然后进行化简求解.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
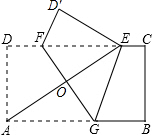 如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.
如图,已知矩形纸片ABCD,AD=2,AB=4,将纸片折叠,使顶点A与边CD上的点E重合,折痕FG分别与AB,CD交于点G、F、AE与FG交于点O.求证:A,G,E,F四点围成的四边形是菱形.