题目内容
13.三角形的三边情况是①a=5,b=12,c=9,②a=15,b=17,c=8,③a=1,b=$2\sqrt{2}$,c=3,④a:b:c=5:12:13,其中直角三角形有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 求证是否为直角三角形,这里给出三边的长,只要验证两小边的平方和等于最长边的平方即可.
解答 解:①52+92≠122,不能构成直角三角形;
②152+82=172,能构成直角三角形;
③12+(2$\sqrt{2}$)2=32,能构成直角三角形;
④设a=5x,b=12x,c=13x,且(5x)2+(12x)2=(13x)2,能构成直角三角形.
故可以构成直角三角形的边长有3个.
故选C.
点评 本题考查了勾股定理的逆定理,在应用勾股定理的逆定理时,应先认真分析所给边的大小关系,确定最大边后,再验证两条较小边的平方和与最大边的平方之间的关系,进而作出判断.

练习册系列答案
 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案
相关题目
5.下列说法中,正确的是( )
| A. | 整数和分数统称为有理数 | |
| B. | 最小的有理数是0 | |
| C. | 正整数、负整数、正分数、负分数统称为有理数 | |
| D. | 0不是有理数 |
2.某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5个参赛者的得分情况.
(1)参赛者F得76分,他答对了几道题?
(2)参赛者G说他得80分,你认为可能吗?为什么?
| 参赛者 | 答对题数 | 答错题数 | 得分 |
| A | 20 | 0 | 100 |
| B | 19 | 1 | 94 |
| C | 18 | 2 | 88 |
| D | 14 | 6 | 64 |
| E | 10 | 10 | 40 |
(2)参赛者G说他得80分,你认为可能吗?为什么?
3.下列方程变形正确的是( )
| A. | 方程$\frac{x-1}{0.2}-\frac{x}{0.5}$=1化成$\frac{10x-10}{2}-\frac{10x}{5}$=10 | |
| B. | 方程3-x=2-5(x-1),去括号,得3-x=2-5x-1 | |
| C. | 方程$\frac{2}{3}t=\frac{3}{2}$,未知数系数化为1,得t=1 | |
| D. | 方程3x-2=2x+1移项得3x-2x=1+2 |
 分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图的平面图形,那么这个几何图形是( )
分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图的平面图形,那么这个几何图形是( )



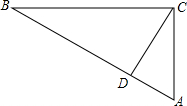 已知:如图,在△ABC中,∠A=60°,CD⊥AB,BC=2CD,AD=$\sqrt{3}$,求AB的长.
已知:如图,在△ABC中,∠A=60°,CD⊥AB,BC=2CD,AD=$\sqrt{3}$,求AB的长.