题目内容
3.已知一个多边形共有35条对角线,求:(1)这个多边形是几边形?
(2)这个多边形内角和的度数是多少?
分析 (1)设这个正多边形是n边形,根据n边形共有对角线$\frac{n(n-3)}{2}$条,即可列出方程:$\frac{n(n-3)}{2}$=35,求解即可;
(2)根据多边形的内角和为:(n-2)×180°,可求出其内角和.
解答 解:(1)设这个正多边形是n边形,根据题意得:
$\frac{n(n-3)}{2}$=35,
解得n1=10,n2=-7(不符题意,舍去).
故这个多边形是十边形;
(2)(10-2)×180°
=8×180°
=1440°.
故这个多边形内角和的度数是1440°.
点评 本题考查了多边形的对角线,多边形内角与外角.用到的知识点:n边形共有对角线$\frac{n(n-3)}{2}$条;多边形的内角和为:(n-2)×180°.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
2.某电视台组织知识竞赛,共设20道选择题,各题分值相同,每题必答.下表记录了5个参赛者的得分情况.
(1)参赛者F得76分,他答对了几道题?
(2)参赛者G说他得80分,你认为可能吗?为什么?
| 参赛者 | 答对题数 | 答错题数 | 得分 |
| A | 20 | 0 | 100 |
| B | 19 | 1 | 94 |
| C | 18 | 2 | 88 |
| D | 14 | 6 | 64 |
| E | 10 | 10 | 40 |
(2)参赛者G说他得80分,你认为可能吗?为什么?
 如图所示,四边形ABCD中,AD∥BC,四边形ABCD的面积为12,求此四边形ABCD四边的中点组成的四边形EFGH的面积.
如图所示,四边形ABCD中,AD∥BC,四边形ABCD的面积为12,求此四边形ABCD四边的中点组成的四边形EFGH的面积.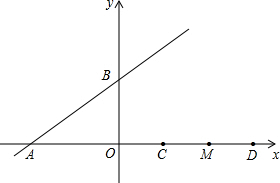 已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧)
已知直线y=$\frac{3}{4}$x+b与x轴,y轴分别交于A,B两点,点D在x轴正半轴,且OD=6,点C,M是线段OD的三等分点(点C在点M的左侧) 如图,四边形ABCD的面积为8cm2,E、F、G、H分别是四条边的中点,求四边形EFGH的面积.
如图,四边形ABCD的面积为8cm2,E、F、G、H分别是四条边的中点,求四边形EFGH的面积. 分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图的平面图形,那么这个几何图形是( )
分别从正面、左面和上面这三个方向看下面的四个几何体,得到如图的平面图形,那么这个几何图形是( )


