Question

1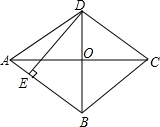．如图，菱形ABCD，AC，BD相交于点O，DE⊥AB，垂足为E，AB=5，OD=3，求AC、DE的长．

Answer 1

分析 由菱形是四条边相等得到AD=AB=5，由菱形的对角线垂直平分得到OD⊥OA，OA=OC，所以在直角△ADO中，利用勾股定理求得OA的长度后，即可得到AC=2OA；由面积法来求DE的长度．

解答 解：在菱形ABCD中，BD⊥AC，AB=AD，AC=2OA，BD=2OD=6，
∵在直角△ADO中，∠AOD=90°，AD=AB=5，OD=3，
∴由勾股定理得到：OA=$\sqrt{A{D}^{2}-O{D}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4，
∴AC=2OA=8．
∴DE⊥AB，垂足为E，
∴AB•DE=$\frac{1}{2}$AC•BD，即5DE=$\frac{1}{2}$×8×6，
解得DE=$\frac{24}{5}$．
综上所述，AC、DE的长分别是8、$\frac{24}{5}$．

点评 此题主要考查了菱形的性质，得出菱形的对角线的长度是解题关键．