题目内容
14. 如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D,抛物线y=$\frac{1}{4}$x2+bx+c经过B、C、D三点.
如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D,抛物线y=$\frac{1}{4}$x2+bx+c经过B、C、D三点.(1)求此抛物线的解析式;
(2)若动直线MN(MN∥x 轴)从点D开始,以每秒1个长度单位的速度沿y轴的正方向移动,且与线段CD、y轴分别交于M、N两点,动点P同时从点C出发,在线段OC上以每秒2个长度单位的速度向原点O运动,连接PM,设运动时间为t秒,
①若以P、C、M为顶点的三角形与△OCD相似,求实数t的值;
②当t为何值时,$\frac{MN•OP}{MN+OP}$的值最大,并求出最大值.
分析 (1)直接利用圆的性质得出B,C点坐标,进而利用交点式求出函数解析式;
(2)①直接利用若△PCM∽△OCD或△MCP∽△OCD,分别得出t的值求出答案即可;
②利用MN∥OC,则$\frac{MN}{DN}$=$\frac{CO}{DO}$,进而求出$\frac{MN•OP}{MN+OP}$关于t的关系式求出最值即可.
解答 解:(1)∵A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,
∴B(-2,0),C(8,0),
代入抛物线y=$\frac{1}{4}$(x+2)(x-8),
得y=$\frac{1}{4}$x2-$\frac{3}{2}$x-4;
(2)①由题可得N(0,t-4),P(8-2t,0),
若△PCM∽△OCD,
则$\frac{PC}{PM}$=$\frac{OC}{OD}$,即$\frac{2t}{4-t}$=$\frac{8}{4}$,
解得t=2;
若△MCP∽△OCD,则$\frac{PC}{MC}$=$\frac{DC}{OC}$,即$\frac{2t}{4\sqrt{5}-\sqrt{5}t}$=$\frac{4\sqrt{5}}{8}$,
解得t=$\frac{20}{9}$,
即当t=2或t=$\frac{20}{9}$时,以P、C、M为顶点的三角形与△OCD相似.
②∵MN∥OC,
∴$\frac{MN}{DN}$=$\frac{CO}{DO}$,即MN=2t,
又∵OP=8-2t,
∴$\frac{MN•PO}{MN+PO}$=$\frac{2t(8-2t)}{2t+8-2t}$=-$\frac{1}{2}$(t-2)2+2,
∴当t=2时取最大值2.
点评 此题主要考查了二次函数综合以及相似三角形的判定与性质,正确利用分类讨论求出t的值是解题关键.

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
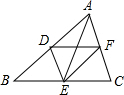 如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )
如图,D、E、F分别是△ABC的边AB、BC、AC的中点.若四边形ADEF是菱形,则△ABC必须满足的条件是( )| A. | AB⊥AC | B. | AB=AC | C. | AB=BC | D. | AC=BC |
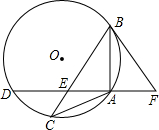 已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.
已知:如图,△ABC内接于⊙O,且AB=AC,点D在⊙O上,AD⊥AB于点A,AD与BC交于点E,F在DA的延长线上,且AF=AE.