Question

4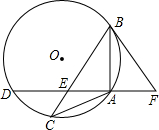．已知：如图，△ABC内接于⊙O，且AB=AC，点D在⊙O上，AD⊥AB于点A，AD与BC交于点E，F在DA的延长线上，且AF=AE．
（1）求证：BF与⊙O相切；
（2）若BF=10，cos∠ABC=$\frac{12}{13}$，求⊙O的半径．

Answer 1

分析 （1）先证明△BEF是等腰三角形，再证明∠FBA+∠DBA=90°即可．
（2）在Rt△BDF中，cosD=$\frac{BD}{DF}=\frac{12}{13}$，设BD=12x，DF=13x，利用勾股定理列出方程即可解决问题．

解答 证明：（1）连接BD，

∵AD⊥AB，
∴∠BAD=90°，
∴BD是直径，BD过圆心，
∵AB=AC，
∴∠ABC=∠C，
∵∠D=∠C，
∴∠ABC=∠D
又∵AD⊥AB，且AF=AE
∴△BEF是等腰三角形，
∴∠ABC=∠ABF，
∴∠D=∠ABF，
又∵∠BAD=90°，
∴∠ABD+∠D=180°-∠BAD=180°-90°=90°，
∴∠ABD+∠ABF=90°，
∴∠DBF=90°，
∴OB⊥BF，
又∵OB是⊙O的半径，
∴BF是⊙OA切线；
（2）∵∠ABC=∠D，
∴cosD=cos∠ABC=$\frac{12}{13}$，
在Rt△BDF中，cosD=$\frac{BD}{DF}=\frac{12}{13}$，设BD=12x，DF=13x，
又∵BD²+BF²=DF²，
∴（12x）²+10²=（13x）²
∵x＞0，
∴x=2，
∴BD=12×2=24，
∴OB=$\frac{1}{2}$BD=12
∴⊙O半径为12．

点评 本题考查圆、切线的判定、勾股定理等知识，灵活运用圆的有关知识是解题的关键，学会证明切线方法，属于中考常考题型．