题目内容
19.计算:(1)-$\sqrt{27}$+$|{\sqrt{3}-2}|$-${(\frac{1}{3})^{-1}}$+2cos60°;
(2)(m+2-$\frac{5}{m-2}$)÷$\frac{m-3}{2m-4}$.
分析 (1)原式利用负整数指数幂法则,二次根式性质,绝对值的代数意义,以及特殊角的三角函数值计算即可得到结果;
(2)原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分即可得到结果.
解答 解:(1)原式=-3$\sqrt{3}$+2-$\sqrt{3}$-3+2×$\frac{1}{2}$=-4$\sqrt{3}$;
(2)原式=$\frac{(m+3)(m-3)}{m-2}$•$\frac{2(m-2)}{m-3}$=2(m+3)=2m+6.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
10.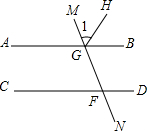 如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )
如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )
 如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )
如图,AB、CD、MN均为直线,AB∥CD,∠GFC=80°,GH平分∠MGB,则∠1的值为( )| A. | 35° | B. | 40° | C. | 45° | D. | 50° |
8. 如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )
如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )
 如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )
如图,AB∥CD,∠B=56°,∠E=22°,则∠D的度数为( )| A. | 22° | B. | 34° | C. | 56° | D. | 78° |
 如图,在Rt△OBC中,OB与x轴正半轴重合,∠OBC=90°,且OC=2,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC,得到△OB2C2,…,如此继续下去,得到△OB2016C2016,则点C2016的坐标为(22016,$\sqrt{3}$•22016).
如图,在Rt△OBC中,OB与x轴正半轴重合,∠OBC=90°,且OC=2,BC=$\sqrt{3}$,将△OBC绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB1=OC,得到△OB1C1,将△OB1C1绕原点O逆时针旋转60°再将其各边扩大为原来的2倍,使OB2=OC,得到△OB2C2,…,如此继续下去,得到△OB2016C2016,则点C2016的坐标为(22016,$\sqrt{3}$•22016). 如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D,抛物线y=$\frac{1}{4}$x2+bx+c经过B、C、D三点.
如图,在平面直角坐标系中,以A(3,0)为圆心,以5为半径的圆与x轴相交于B、C,与y轴的负半轴相交于D,抛物线y=$\frac{1}{4}$x2+bx+c经过B、C、D三点. 菱形ABCD的边长为3m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为$\frac{9}{4}$$\sqrt{3}$m2(结果保留根号).
菱形ABCD的边长为3m,∠A=60°,弧CD是以点B为圆心,BC长为半径的弧,弧BD是以A为圆心,AB长为半径的弧,则阴影部分面积为$\frac{9}{4}$$\sqrt{3}$m2(结果保留根号). 如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)
如图,在矩形ABCD中,E是AD边的中点,BE⊥AC于点F,连接DF,有下列四个结论:①△AEF∽△CAB;②CF=2AF;③tan∠CAD=$\sqrt{2}$;④S四边形CDEF=$\frac{5}{2}$S△ABF,其中正确的结论是①②④.(填写序号即可)