Question

15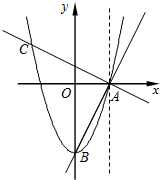．如图，抛物线y=ax²+c经过A（1，0），B（0，-2）两点．连结AB，过点A作AC⊥AB，交抛物线于点C．
（1）求该抛物线的解析式；
（2）求点C的坐标；
（3）将抛物线沿着过A点且垂直于x轴的直线对折，再向上平移到某个位置后此抛物线与直线AB只有一个交点，请直接写出此交点的坐标．

Answer 1

分析 （1）根据抛物线y=ax2+c经过A（1，0），B（0，-2）两点列出a和c的二元一次方程组，求出a和c的值；
（2）首先根据三角形相似的性质求出点D的坐标，设直线AC的解析式是y=kx+b，待定系数法求出直线AC的解析式，进而求出点C坐标；
（3）先求出对折后抛物线的解析式，然后设出向上平移后抛物线的解析式，根据抛物线与直线AB只有一个交点求出k的值，进而求出此时的抛物线解析式，即可求出交点坐标．

解答 解：（1）因为抛物线y=ax²+c经过A（1，0），B（0，-2）两点，
则有：$\left\{\begin{array}{l}{a+c=0}\\{c=-2}\end{array}\right.$
解得：$\left\{\begin{array}{l}{a=2}\\{c=-2}\end{array}\right.$，
所求的抛物线的解析式是：y=2x²-2；

（2）∵AC⊥AB，又根据题意可知：OA⊥BD，
∴Rt△AOD∽Rt△BOA，
∴$\frac{AO}{BO}=\frac{OD}{AO}$，
∴OD=$\frac{A{O}^{2}}{BO}$，
又根据A（1，0），B（0，-2），则有：AO=1，BO=2，
∴OD=$\frac{1}{2}$，
∴D（0，$\frac{1}{2}$），
设直线AC的解析式是y=kx+b，则有
$\left\{\begin{array}{l}{b=\frac{1}{2}}\\{k+b=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{k=-\frac{1}{2}}\\{b=\frac{1}{2}}\end{array}\right.$，
∴所求的解析式是：y=-$\frac{1}{2}$x+$\frac{1}{2}$，
由直线AC与抛物线y=2x²-2相交，则有：
-$\frac{1}{2}$x+$\frac{1}{2}$=2x²-2，
解得：x₁=-$\frac{5}{4}$，x₂=1，
当x=-$\frac{5}{4}$时，y=-$\frac{1}{2}$×（-$\frac{5}{4}$）+$\frac{1}{2}$=$\frac{9}{8}$，
∴点C的坐标是（-$\frac{5}{4}$，$\frac{9}{8}$）；

（3）抛物线沿着过A点且垂直于x轴的直线对折后与x轴的交点坐标为（1，0）和（3，0），
此时抛物线解析式为y=2（x-2）²-2，
向上平移此时解析式为y=2（x-2）²+k，
直线AB的解析式为y=2x-2，
则2（x-2）²+k=2x-2，
△=100-80-8k=0，
解得k=$\frac{5}{2}$，
即2（x-2）²+$\frac{5}{2}$=2x-2，
解得x=$\frac{5}{2}$，
所求交点的坐标是（$\frac{5}{2}$，3）．

点评 本题主要考查了二次函数的综合题，此题涉及到待定系数法求二次函数的解析式，相似三角形的性质、直线与抛物线的交点问题以及二次函数图象的平移等知识，解答本题的关键是熟练掌握二次函数的性质以及翻折变换以及平移的知识，此题有一定的难度．