题目内容
20.已知x1、x2是关于x一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根,且(3x1-x2)(x1-3x2)=-80,则实数a的值为-$\frac{33}{5}$.分析 首先根据根的判别式求出a的取值范围,然后把(3x1-x2)(x1-3x2)=-80转化为5a2-18a-99=0,结合a的取值范围求出a的值.
解答 解:∵x1、x2是关于x一元二次方程x2+(3a-1)x+2a2-1=0的两个实数根,
∴△=(3a-1)2-4(2a2-1)=a2-6a+5≥0,
∴a≥5或a≤1,
∴x1+x2=1-3a,x1、x2=2a2-1,
∵(3x1-x2)(x1-3x2)=-80,
∴3x12-10x1x2+3x22=-80,
∴3(x1+x2)2-16x1x2=-80,
∴5a2-18a-99=0,
∴(5a+33)(a-3)=0,
∴a1=-$\frac{33}{5}$,a2=3,
∵a≥5或a≤1,
∴a=-$\frac{33}{5}$,
故答案为-$\frac{33}{5}$.
点评 本题主要考查了根与系数的关系的知识,解答本题的关键是根据根与系数的关系把(3x1-x2)(x1-3x2)=-80转化为5a2-18a-99=0,此题难度不大,但是很容易出现错误.

练习册系列答案
相关题目
10.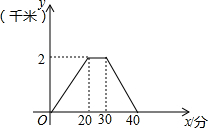 星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
(1)小王去时的速度大于回家的速度;
(2)小王在朋友家停留了10分;
(3)小王去时所花的时间少于回家所花的时间;
(4)小王去时走上坡路,回家时走下坡路.
 星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )
星期天,小王去朋友家借书,如图是他离家的距离y(千米)与时间x(分)的函数图象,根据图4信息,下列说法正确的是( )(1)小王去时的速度大于回家的速度;
(2)小王在朋友家停留了10分;
(3)小王去时所花的时间少于回家所花的时间;
(4)小王去时走上坡路,回家时走下坡路.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
5.把分式$\frac{x+y}{x-3y}$中的x和y都扩大为原来的2倍,则分式的值( )
| A. | 不变 | B. | 扩大为原来的2倍 | C. | 缩小为原来的$\frac{1}{2}$ | D. | 扩大为原来的4倍 |
10.-2的相反数是( )
| A. | 2 | B. | -2 | C. | $-\frac{1}{2}$ | D. | $\frac{1}{2}$ |
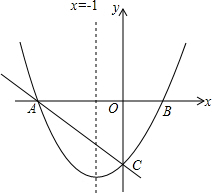 如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.
如图:对称轴x=-1的抛物线y=ax2+bx+c(a≠0)与x轴相交于A,B两点,其中点A的坐标为(-3,0),且点(2,5)在抛物线y=ax2+bx+c上.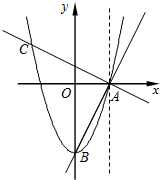 如图,抛物线y=ax2+c经过A(1,0),B(0,-2)两点.连结AB,过点A作AC⊥AB,交抛物线于点C.
如图,抛物线y=ax2+c经过A(1,0),B(0,-2)两点.连结AB,过点A作AC⊥AB,交抛物线于点C.