如果$\frac{x}{x-3}$=2+$\frac{3}{x-3}$有增根.那么增根为x=3．题目和参考答案——青夏教育精英家教网—

题目内容

7．如果$\frac{x}{x-3}$=2+$\frac{3}{x-3}$有增根，那么增根为x=3．

分析增根是分式方程化为整式方程后产生的使分式方程的分母为0的根．有增根，最简公分母x-3=0，所以增根是x=3．

解答解：∵方程有增根，
∴方程最简公分母为x-3=0，即增根是x=3，
故答案为x=3．

点评本题考查了分式方程的增根，解决增根问题的步骤：
①确定增根的值；
②化分式方程为整式方程；
③把增根代入整式方程即可求得相关字母的值．

练习册系列答案

$\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$

B．

$\sqrt{2}$×$\sqrt{3}$=$\sqrt{6}$

C．

$\sqrt{8}$+$\sqrt{2}$=2

D．

（-$\sqrt{3}$）²=3

15．

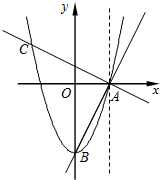如图，抛物线y=ax²+c经过A（1，0），B（0，-2）两点．连结AB，过点A作AC⊥AB，交抛物线于点C．
（1）求该抛物线的解析式；
（2）求点C的坐标；
（3）将抛物线沿着过A点且垂直于x轴的直线对折，再向上平移到某个位置后此抛物线与直线AB只有一个交点，请直接写出此交点的坐标．

2．

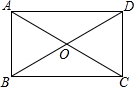如图，在四边形ABCD中，点O是AC的中点，
（1）若AB∥CD，求证：△OAB≌△OCD；
（2）在问题（1）中，若AC=BD，则四边形ABCD是矩形．

12．定义：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S_△ACD=S_△BCD．应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF与BE交于点O．
（1）求证：△AOB和△AOE是“友好三角形”；
（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．

19．

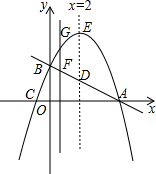如图，已知直线y=-$\frac{1}{2}$x+2与坐标轴交于A、B两点，抛物线y=-x²+bx+c与x轴交于A、C两点，与y轴交于点B．
（1）求b、c的值．
（2）平行于y轴的直线x=2交直线AB于点D，交抛物线于点E．
①点P从原点O出发，沿x轴正方向以1个单位/秒的速度运动，设运动时间为t，过点P作x轴的垂线与直线AB交于点F，与抛物线交于点G，当t为何值时，FG：DE=1：2？
②将抛物线向上平移m（m＞0）个单位后与y轴相交于点B′，与直线x=2相交于点E′，当E′O平分∠B′E′D时，求m的值．

16．下列二次根式中能与$\sqrt{2}$合并的二次根式的是（　　）

17．

如图，⊙O的半径长6cm，点C在⊙O上，弦AB垂直平分OC于点D，则弦AB的长为（　　）

试题分类