题目内容
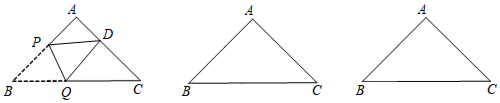
17.如图,在Rt△ABC中,∠A=90°,AB=AC=2cm,将△ABC折叠,使点B落在射线CA上点D处,折痕为PQ.(1)当点D与点A重合时,求PQ长;
(2)当点D与C、A不重合时,设AD=xcm,AP=ycm.
①求y与x的函数关系式,并写出x的取值范围;
②当重叠部分为等腰三角形时,请直接写出x的值.
分析 (1)由折叠得出PQ是AB的垂直平分线,进而得出PQ是△ABC的中位线,即可得出结论;
(2)①由折叠得出PD=BP=2-y,再用勾股定理建立方程即可得出结论;
②根据等腰三角形的定义,分①PD=DQ时,BP=BQ,再根据翻折变换前后的线段相等判断出BP=BQ=PD=DQ,从而得到四边形BQDP是菱形,根据菱形的对边平行可得PD∥BC,BP∥DQ,然后判断出△APD和△CDQ都是等腰直角三角形,根据等腰直角三角形的性质用AD表示出PD、CD,然后根据AC的长度列方程求解即可;②DQ=PQ时,BQ=PQ,求出△BPQ是等腰直角三角形,点B与点C重合,从而得到AD=AC;③PD=PQ时,PQ=BP,然后求出△BPQ是等腰直角三角形,点B与点A重合,不符合题意.
解答 解:(1)如图,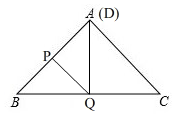
当点D和点A重合时,
由折叠知,AP=BP,∠BPQ=∠APQ,
∵∠APQ+∠BPQ=180°,
∴∠BPQ=∠APQ=90°=∠BAC,
∴PQ∥AC,
∵AP=BP,
∴PQ是△ABC的中位线,
∴PQ=$\frac{1}{2}$AC=1;
(2)①∵AD=x,AC=2,
∴CD=2-x,
∵AP=y,AB=2,
∴BP=2-y,
在△ABC中,∠BAC=90°,AC=AB=2,
∴BC=2$\sqrt{2}$,∠B=∠C=45°,
如图1,
由折叠知,DP=BP=2-y,
在Rt△ADP中,根据勾股定理得,AP2+AD2=PD2,
∴y2+x2=(2-y)2,
∴y=-$\frac{1}{4}$x2+1(0≤x≤2);
②、Ⅰ、PD=DQ时,BP=BQ,
由翻折变换得,BP=PD,BQ=DQ,
∴BP=BQ=PD=DQ,
∴四边形BQDP是菱形,
∴PD∥BC,BP∥DQ,
∵∠A=90°,AB=AC,
∴△ABC是等腰直角三角形,
∴△APD和△CDQ都是等腰直角三角形,
在Rt△APD中,PD=$\sqrt{2}$AD=$\sqrt{2}$x,
在Rt△CDQ中,CD=DQ,
∵PD=DQ,
∴CD=$\sqrt{2}$AD,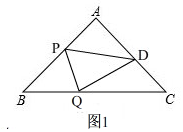
∵AC=AD+CD,
∴AD+$\sqrt{2}$AD=2,
即:x+$\sqrt{2}$x=2
解得AD=2$\sqrt{2}$-2;
Ⅱ、DQ=PQ时,BQ=PQ,
∴∠BPQ=∠B=45°,
∴△BPQ是等腰直角三角形,
∴点B与点C重合,
∴x=AD=AC=2;
Ⅲ、PD=PQ时,PQ=BP,
∴∠BQP=∠B=45°,
∴△BPQ是等腰直角三角形,
∴点B与点A重合,
此时,点B与点A重合,不符合题意,舍去;
综上所述,AD的长度为2或2$\sqrt{2}$-2.
点评 此题是几何变换综合题,主要考查了等腰直角三角形的性质,折叠的性质,三角形的中位线定理,勾股定理,等腰三角形的性质,解(1)的关键是得出PQ是AB的垂直平分线,解(2)①的关键是利用勾股定理建立方程,解(2)②的关键是分类讨论思想,是一道中考常考题.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案| A. | 一个解 | B. | 两个解 | C. | 一个或两个解 | D. | 无解 |
| A. | 车辆随机到达一个路口,遇到红灯 | |
| B. | 两条线断可以组成一个三角形 | |
| C. | 400人中有两个人的生日在同一天 | |
| D. | 掷一枚质地均匀的骰子,掷出的点数是质数 |
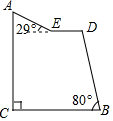 “蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736)
“蘑菇石”是我国著名的自然保护区梵净山的标志,小明从山脚B点先乘坐缆车到达观景平台DE观景,然后再沿着坡脚为29°的斜坡由E点步行到达“蘑菇石”A点,“蘑菇石”A点到水平面BC的垂直距离为1890m.如图,DE∥BC,BD=1800m,∠DBC=80°,求斜坡AE的长度.(结果精确到0.1m,可参考数据sin29°≈0.4848,sin80°≈0.9848,cos29°≈0.8746,cos80°≈0.1736) 将如图所示的正方体的展开图进行折叠后可以围成正方体,则正方体中EF的位置正确的是( )
将如图所示的正方体的展开图进行折叠后可以围成正方体,则正方体中EF的位置正确的是( )



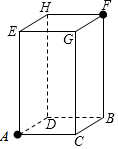 一只蚂蚁如果沿长方体的表面从A点爬到F点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.
一只蚂蚁如果沿长方体的表面从A点爬到F点,那么沿哪条路最近,最短的路程是多少?已知长方体的长2cm、宽为1cm、高为4cm.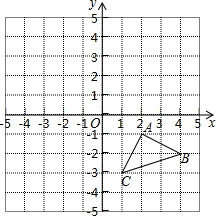 三角形ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将三角形ABC平移至三角形A1B1C1的位置,点A、B、C对应的点分别为A1,B1,C1,已知点A1的坐标是(-2,3).
三角形ABC的三个顶点坐标分别为A(2,-1),B(4,-2),C(1,-3),将三角形ABC平移至三角形A1B1C1的位置,点A、B、C对应的点分别为A1,B1,C1,已知点A1的坐标是(-2,3).