题目内容
12.关于x的方程(a+3)x2-5x=0的解的情况是( )| A. | 一个解 | B. | 两个解 | C. | 一个或两个解 | D. | 无解 |
分析 分类讨论:①当3+a=0即a=-3时,此时方程为一元一次方程,方程有一个实数根;②当3+a≠0即a≠-3时,此时方程为一元二次方程,利用根的判别式判断根的情况.
解答 解:①当3+a=0即a=-3时,此时方程为一元一次方程,方程有一个实数根;
②当3+a≠0即a≠-3时,此时方程为一元二次方程,
△=(-5)2-4×(a+3)×0=25>0,
∴原方程有两个实数根,
综上所述,原方程有一个或两个解,
故选C.
点评 本题主要考查了根的判别式,利用分类讨论思想是解答此题的关键.

练习册系列答案
相关题目
20.对于任意整数n,多项式(4n+5)2-9都能( )
| A. | 被6整除 | B. | 被7整除 | C. | 被8整除 | D. | 被6或8整除 |
1. 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
 如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )
如图,在△ABC中,DE∥BC,若AD=3,BD=4,BC=5,则DE的长为( )| A. | $\frac{15}{4}$ | B. | $\frac{15}{7}$ | C. | $\frac{12}{5}$ | D. | $\frac{5}{2}$ |
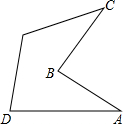 某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号).
某地铁站口的垂直截图如图所示,已知∠A=30°,∠ABC=75°,AB=BC=4米,求C点到地面AD的距离(结果保留根号).