题目内容
2.(1)解不等式组:$\left\{\begin{array}{l}{4x>2x-6}\\{\frac{x-1}{3}≤\frac{x+1}{9}}\end{array}\right.$,并把解集在数轴上表示出来.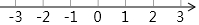
(2)先化简,再求值:(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$,其中x=tan60°+(-$\frac{1}{2}$)-2+50-$\sqrt{3}$.
分析 (1)先求出每个不等式的解集,再根据找不等式组解集的规律找出不等式组的解集即可;
(2)利用分式的混合运算,化简原式,再把当x=tan60°+(-$\frac{1}{2}$)-2+50-$\sqrt{3}$,代入化简后的式子,计算即可.
解答 解:(1)$\left\{\begin{array}{l}{4x>2x-6①}\\{\frac{x-1}{3}≤\frac{x+1}{9}②}\end{array}\right.$,
∵解不等式①得:x>-3,
解不等式②得:x≤2,
∴不等式组的解集为-3<x≤2,
在数轴上表示不等式组的解集为: ;
;
(2)(1-$\frac{1}{x-1}$)÷$\frac{{x}^{2}-4x+4}{{x}^{2}-1}$=$\frac{x-2}{x-1}$•$\frac{(x+1)(x-1)}{(x-2)^{2}}$=$\frac{x+1}{x-2}$,
当x=tan60°+(-$\frac{1}{2}$)-2+50-$\sqrt{3}$=5时,
原式=2.
点评 本题考查了分式的化简求值、特殊三角函数值的知识,解决此类题目的关键是熟记特殊角的三角函数值.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
2.永州市是一个降水丰富的地区,今年4月初,某地连续降雨导致该地某水库水位持续上涨,下表是该水库4月1日~4月4日的水位变化情况:
(1)请建立该水库水位y与日期x之间的函数模型;
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
| 日期x | 1 | 2 | 3 | 4 |
| 水位y(米) | 20.00 | 20.50 | 21.00 | 21.50 |
(2)请用求出的函数表达式预测该水库今年4月6日的水位;
(3)你能用求出的函数表达式预测该水库今年12月1日的水位吗?
13.某登山队从大本营出发,在向上攀登的过程中,测得所在位置的气温y℃与向上攀登的高度x km的几组对应值如表:
若每向上攀登1km,所在位置的气温下降幅度基本一致,则向上攀登的海拔高度为2.5km时,登山队所在位置的气温约为-10℃.
| 向上攀登的高度x/km | 0.5 | 1.0 | 1.5 | 2.0 |
| 气温y/℃ | 2.0 | -0.9 | -4.1 | -7.0 |
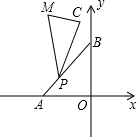 如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度.
如图,A(-3,0),B(0,3),C(-1,4),P,C,M按逆时针顺序排列,动点P在线段AB上,∠C=90°,∠CPM=30°,请求出当P点从A运动到B点时,点M运动的路径时什么?并求出M点运动路径长度. 如图,已知△ABC≌△DEF,∠A=32°,∠B=48°,BF=3,求∠DFE的度数和EC的长.
如图,已知△ABC≌△DEF,∠A=32°,∠B=48°,BF=3,求∠DFE的度数和EC的长.