题目内容
20.(1)$\frac{-14m{n}^{2}k}{4{m}^{2}n}$(2)m-1+$\frac{2m-6}{{m}^{2}-9}$÷$\frac{2m+2}{m+3}$
(3)$\frac{1-x}{x-2}$=$\frac{1}{2-x}$-2
(4)$\frac{1}{2-x}$=$\frac{1}{x-2}$-$\frac{6-x}{3{x}^{2}-12}$.
分析 (1)原式约分即可得到结果;
(2)原式先计算除法运算,再计算加减运算即可;
(3)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解;
(4)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=-$\frac{7nk}{2m}$;
(2)原式=m-1+$\frac{2(m-3)}{(m+3)(m-3)}$•$\frac{m+3}{2(m+1)}$=m-1+$\frac{1}{m+1}$=$\frac{{m}^{2}}{m+1}$;
(3)去分母得:1-x=-1-2x+4,
解得:x=2,
经检验x=2是增根,分式方程无解;
(4)去分母得:-3x-6=3x+6-6+x,
解得:x=-$\frac{6}{7}$,
经检验x=-$\frac{6}{7}$是分式方程的解.
点评 此题考查了解分式方程,以及分式的混合运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
12.某校计划修建一座既是中心对称图形又是轴对称图形的花坛,从学生中征集到设计方案有等腰三角形、正三角形、平行四边形、菱形等四种图案,你认为符合条件的是( )
| A. | 等腰三角形 | B. | 正三角形 | C. | 平行四边形 | D. | 菱形 |
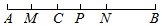 如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点.
如图,点C是线段AB上一点,点M,N,P分别是线段AC,BC,AB的中点. 如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.
如图,折线ABC是在某市乘出租车所付车费y(元)与行车里程x(km)之间的函数关系图象.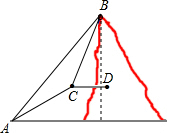 如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°,于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?
如图,小明和小强攀登一无名山峰,他俩在山脚A处测得主峰B的仰角为45°,然后从山脚沿一段倾角为30°的斜坡走了2km到达山腰C,此时测得主峰B的仰角为60°,于是小明对小强说:“我知道主峰多高了.”你能根据他们的数据算出主峰的高度吗?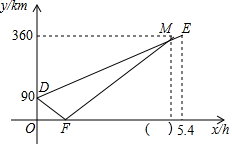 A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题:
A,B,C三地在同一条公路上,A地在B,C两地之间,甲、乙两车同时从A地出发匀速行驶,甲车驶向C地,乙车先驶向B地,到达B地后,调头按原速经过A地驶向C地(调头时间忽略不计),到达C地停止行驶,甲车比乙车晚0.4小时到达C地,两车距B地的路程y(km)与行驶时间x(h)之间的函数关系如图所示,请结合图象信息,解答下列问题: